球環

球環是一種特殊的球檯，是平面上一小於半圓的弓形繞不穿過它的直徑旋轉一周所生成的幾何體。也可以將球環看成是從球檯內截去一個與球檯共底的圓台或圓柱而成的幾何體 。

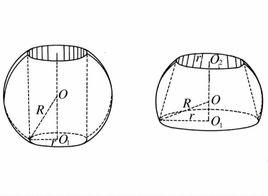
球環的概念

將一弓形繞不穿過它的一條直徑旋轉，所產生的立體稱為 球 環。弓形是指由一段圓弧與它所對弦所圍成的圖形。當弧是劣弧時，稱為劣弓形，否則稱為優弓形。如圖1中的球環就是球檯去掉中間的圓柱，圖2中的球環就是球檯去掉中間的圓台 。

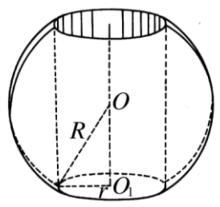圖1

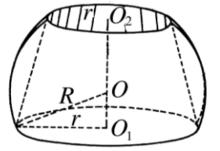圖2

相關定理

球環的體積 弓形繞不穿過它的直徑旋轉時，所產生的體積(球環的體積)是一個柱的體積的六分之一，這個柱的底是以弓形的弦為半徑的圓，高則為這弦在軸上的射影 。

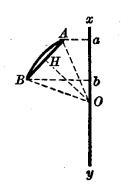圖3

證明 設一圓O(圖3)的弧AB及其弦所園的弓形繞通過O的軸xy旋旋，仍設ab為AB在xy上的射影。

當圖形繞xy旋轉時，圓扇形OAB產生的體積等於

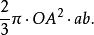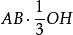球環

球環

另一方面，三角形OAB旋轉時產生的體積等於面積(以OH表示圓心到弦AB的距離)，即等於

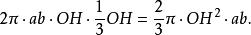球環

上面兩個體積的差顯然由球環的體積構成，因此它等於

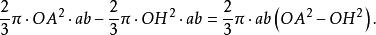球環

但在三角形OAH中有

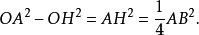球環

所以

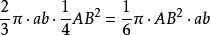球環

球環AB的體積=，證畢 。