定義
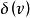狄拜理論愛因斯坦比熱理論中把各格點的振動看作是完全獨立的。事實上，每一個格點的運動都和周圍的格點緊密相關，應該當作一個整體來看待。德拜(1912年)根據整體運動的特點，把晶格看作是各向同性的連續介質，把晶格的振動看作是連續介質中傳播的彈性波。 知道了單位率間隔內的彈性波的支數f(v)，頻率為ν的彈性波的平均能量 ，可求出總能量
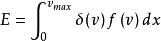狄拜理論對溫度T微分即可算出比熱。
在德拜理論中
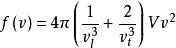狄拜理論
狄拜理論
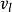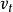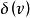狄拜理論
狄拜理論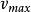 狄拜理論
狄拜理論是體積， 和 分別是介質中縱波和橫波的速度。 同樣可考慮到能量量子化，用統計方法算出。許可的頻率上限 由條件
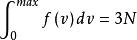狄拜理論決定。N個原子組成的固體。自由度總數是3N，存在的彈性波的數目最多也只能有3N支。
為了簡化比熱公式，引入德拜溫度
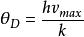狄拜理論最後得到摩爾熱容
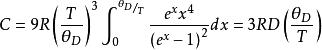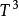狄拜理論
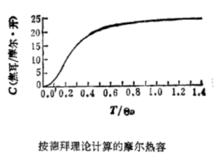
狄拜理論其中D(x)叫德拜函式。在高溫區摩爾熱容趨近經典值3R，在低溫區隨溫度按 規律變化。和實驗一致，如下圖。
狄拜理論按照徳拜理論，只要知道某物質的德拜溫度，即可求出各個溫度下的比熱值，並和實驗基本符合。此方法簡便可靠，因此得到了廣泛的套用。以後的研究發現，徳拜理論仍存在一定的偏差，其原因是忽略了晶格的分立性，仍然是一個比較簡單的模型。
相關理論
德拜
狄拜理論德拜( Peter Joseph Wilhelm Debye,1884~1966)美國物理學家，原籍荷蘭。慕尼黑大學哲學博士。曾任烏得勒支大學、格廷根大學、蘇黎世國立工業大學、菜比錫大學、康奈爾大學教授。提出固體比熱理論,得到理論和隨固體而異的德拜溫度。1916年與瑞士物理學家謝樂(Paul Scherrer,1890~)合作創立晶體粉末的X射線衍射法(德拜-謝樂法)，用於研究晶體的結構。還提出關於強電解質溶液的理論、高分子溶液理論、光的散射理論、粘度理論等，指出用絕熱去磁法可獲得極低的低溫。因他提出極化分子理論和對測定分子結構所作的貢獻，獲1936年諾貝爾化學獎。著有《極性分子》等。
德拜模型
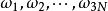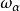狄拜理論
狄拜理論愛因斯坦把N個原子的晶格振動歸結為3N個獨立的諧振動，這些諧振動的圓頻率ω相同，這種模型過於簡單。實際上，晶格原子之間有不可急略的相互作用，不是彼此獨立，原子作非常複雜的耦合振動。德拜理論認為，原子的振動在固體中形成駐波，駐波的圓頻率為 ，某個原子的振動是這些駐波在該原子處引起的振動的合成。圓頻率為 。的駐波的能量與個諧振子的能量相同。
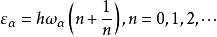狄拜理論根據上式，這種駐波的平均能量為
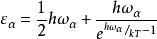狄拜理論這樣，包含N個原子的固體，其晶格振動的總能量為
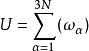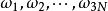狄拜理論 狄拜理論根據此式,如果已知駐波的圓頻率 ，則可算出晶格振動的總能量U。從形式上看，這似乎已經解決了問題，但這樣一來理論的待定參數就有3N個之多，實際上沒有意義。德拜提出的頻譜分布解決了這個問題。
德拜頻譜
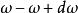狄拜理論參照輻射空腔內電磁駐波的情形，固體中彈性駐波的圓頻率雖然取分立值，但也很密集，在定量計算時也可當作連續變數處理。設圓頻率在 內的駐波數目為，應有
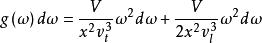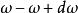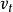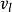狄拜理論 狄拜理論 狄拜理論 狄拜理論 狄拜理論式中第一項是彈性駐波中圓頻率在 內的橫波數目，和電磁駐波的情形完全相同，其中 是固體中橫波波速。固體中除了橫波外還可以有彈性縱波，式中第二項就是關於縱波的。縱波只有一個振動方向，不像橫波有兩個獨立的振動方向，所以縱波數目比橫波少一半。式中 是縱波波速， 是給定固體塊體積。
狄拜理論
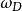狄拜理論
狄拜理論上式對 積分應當給出駐波數目3N，積分上限取為 顯然不合適，德拜引入一最高圓頻率 ，使得
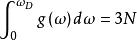狄拜理論積分後可求得
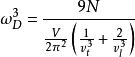狄拜理論可改寫成
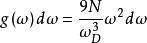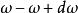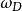狄拜理論 狄拜理論 狄拜理論這就是德拜頻譜。它表示圓頻率在 內的駐波數目。式中N是給定固體塊中的原子數， 叫德拜頻率，是德拜理論中的待定參量。通常用德拜溫度的形式來表示它，即，令
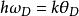狄拜理論
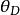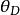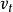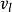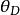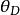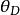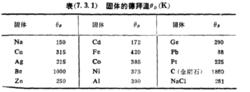
狄拜理論 狄拜理論 狄拜理論 狄拜理論 狄拜理論 狄拜理論 狄拜理論叫德拜溫度， 可以由彈性波在固體中的傳播速度 和 通過公式式而求得，也可以由熱容量的實驗數據確定。兩種方法給出的 的數值相差不多。德拜溫度 已成為固體的一個特性常數。下圖列出了一些物質的 的數值，是由熱容量實驗定出的。
狄拜理論