科學解析
在經典控制理論中，對一個線性定常系統，可用常微分方程或傳遞函式加以描述，可將某個單變數作為輸出，直接和輸入聯繫起來。實際上系統除了輸出量這個變數之外，還包含有其它相互獨立的變數，而微分方程或傳遞函式對這些內容的中間變數是不便描述的，因而不能包含系統的所有信息。顯然，從能否完全揭示系統的全部運動狀態來說，用微分方程或傳遞函式來描述一個線性定常系統有其不足之處。
在用狀態空間法分析系統時，系統的動態特性是用由狀態變數構成的一階微分方程組來描述的。它能反映系統的全部獨立變數的變化，從而能同時確定系統的全部內部運動狀態，而且還可以方便地處理初始條件。這樣，在設計控制系統時，不再只局限於輸入量、輸出量、誤差量，為提高系統性能提供了有力的工具。加之可利用計算機進行分析設計及實時控制，因而可以套用於非線性系統、時變系統、多輸入—多輸出系統以及隨機過程等。
方程式
狀態方程和輸出方程合起來，構成一個系統完整的動態描述稱為系統的狀態空間表達式。
在經典控制理論中，用指定某個輸出量的高階微分方程來描述系統的動態過程。
同一系統中，狀態變數選取的不同，狀態方程也不同。
從理論上說，並不要求狀態變數在物理上一定是可以測量的量，但在工程實踐上，仍以選取那些容易測量的量作為狀態變數為宜，因為在最優控制中，往往需要將狀態變數作為反饋量。
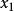狀態空間表達式 
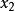狀態空間表達式 
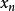狀態空間表達式 設單輸入—單輸出定常系統，其狀態變數為 ， ，…， ，用矢量矩陣表示時的狀態空間表達式則為：
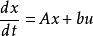狀態空間表達式 
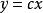狀態空間表達式 對於多輸入—多輸出系統狀態空間表達式的矢量矩陣形式為：
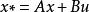狀態空間表達式 
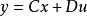狀態空間表達式 連續系統的狀態空間表達式狀態方程是由控制系統的狀態變數和控制變數構成的一階微分方程組。 輸出方程是該系統輸出變數與狀態變數和控制變數的函式關係式。它們一般表示為 狀態方程 輸出方程 無二f(x，u，t) y~g(x，u，t) (1) 式中f，g為向量函式;x為n維狀態向量;u為P維控 制向量;t為時間變數;戈為狀態變數關於t的一階微 分向量;y為q維輸出向量。 如果所描述的控制系統是線性的，則狀態空間表 達式為 毖=A(t)x十B(t)u y=C(t)x+D(t)u (2) 式中x任尺”;夕〔Rq;u〔尺p。通常，，《n，P簇n，A(t)為， xn維系統矩陣，B(t)為n只P維輸人矩陣，c(t)為qx n維輸出矩陣，D(t)為q火p維前饋矩陣。 如果式(1)中的函式f、g或式(2)中的A、B、 C、D不依賴於時間變數t，則該控制系統是定常的。線 性定常控制系統的狀態空間表達式為 x一Ax+方“ y~Cx十Du 式中矩陣A、B、C和D均為常數矩陣。圖為式 示的狀態空間表達式表述的控制系統的框圖。 (3) (2)所 D(t) B(，)卜吠終 C(，)卜~落 A(I) 狀態空間表達式的系統框圖 線性離散時間系統的狀態空間表達式線性離散 時間系統的狀態空間表達式為 x(kT十T)一G(kT)x(kT)+H(kT)u(kT) y(kT)一C(kT)x(kT)+D(kT)u(kT) (4) 式中k一O，1，2，…;T為採樣周期;x任R”;“任R“; 夕任尺p;G，萬，e，D為適當的維數。 如果控制系統又是定常的，則其狀態空間表達式 為 x(kT+T)~Gx(kT)+Hu(kT) y(kT)=C工(kT)十Du(kT) 狀態空間表達式的非唯一性及其變換 (5) 描述一個 給定控制系統的狀態向量不是唯一的，即可以選擇不 同的狀態向量。因此，其狀態空間表達式也不是唯一 的。以線性定常連續控制系統為例，對其狀態向量x 作線性變換，使得x一T蕪，其中T為任何非奇異n又n 維矩陣。若以牙為狀態向量，則該系統的狀態空間表 達式為 x一Ax+B“) __卜(6) y~Cx十刀“) 式中又一T一‘AT;石一r一‘B;亡~cT;萬一D。上述變換 一乃91- 也稱為坐標變換或基底變換。一個控制系統的狀態空 間表達式可以有許多不同的形式，但所有表達式的系 統矩陣的特徵值是不變的。一個n維的控制系統(即系 統矩陣A為二xn維矩陣)有且僅有n個特徵值。對實 常數矩陣A而言，其。個特徵值或為實數，或為 共扼複數對。如果A是實對稱陣，則其特徵值必為實數。為 了分析和綜合的簡便，規定了稱為規範型的幾種狀態 空間表達式。 狀態空間表達式的求解對於線性定常控制系 統，如果假定它的初始狀態x(0)一。，那么進行拉普拉 斯變換後其狀態空間表達式可以表示為 X(s)=(51一A)一‘BU(s) Y(s)=仁C(51一A)一’B+D〕U(s) (7) 式中I為nxn維單位矩陣;，為復變數;(sI一A)一’B一 Wx(s)，稱為輸人一狀態傳遞函式矩陣;C(sI一A)一‘B +D一w(s)，稱為輸人一輸出傳遞函式矩陣〔不少文獻 中記作G(:)〕。一個線性定常控制系統的輸人一輸出傳 遞函式矩陣是不隨狀態空間表達式的不同而改變的。 對狀態空間表達式求解就是解一階微分方程組。 假定狀態空間表達式有解且有唯一的解，則式(2)所 示線性時變控制系統狀態空間表達式的解為x(t) 一，(才，!。，·(!。，+丈。，(才，·，B(·，·(·，d一式中前面- 部分是初始時刻狀態x(t。)的轉移，後面一部分是由控 料作用激勵的轉移。女口式(3)所示的線性定常控制索 統狀態空間表達式的解為x(t)一山(t一t。)x(t。)十 {:。，(卜·，B·(·，d一，(才，才。，和，‘卜·，稱為毗轉 移矩陣。 連續系統狀態空間表達式的離散化在利用計算 機求解連續時間控制系統的狀態空間表達式時，或者 對連續受控對象實行計算機控制時，可以把連續時間 控制系統變換為離散時間控制系統。這時兩個狀態空 間表達式之間滿足如下條件 、|||﹄||IJ G(kT)~中仁(k+1)T，kT口 H(‘T，一{ (k+l)T 山[(k+1)T，二]召(:)d: (8) c(無了’)~[e(t)j，_是二 D(kT)一〔D(t)〕，_二 如式(4)所示的初始時刻為hT的線性離散時變控制 系統狀態空間表達式的解為x(kT)一。(kT，hT)火 k一1 x(hT)斗、三必〔kT，(‘+1)T〕H(汀)u(iT)·如式(5)所 示的初始時刻為hT的線性離散定常控制系統狀態空 間表達式的解為 Hu(乞T)。 k一1 x(kT)=G厄x(hT)+藝G〔k一(‘+’)〕又 菌~h 控制系統的實現對於結構和參數已知的控制系 統，可以根據系統運動的規律(物理的、化學的、生物 的或社會的等)直接建立其狀態空間表達式。例如，根 據框圖或高階微分方程式建立系統的狀態空間表達 式。但如果系統內部結構不知道或不完全知道，也得不 到它的高階微分方程式，則需要用其他的方法建立。可 行的辦法是由實驗確定系統的輸人一輸出特性，例如傳 遞函式矩陣或衝激回響函式陣，然後導出相應的狀態 空間表達式。這樣的方法稱為實現問題。 對於線性定常控制系統，實現問題的基本屬性 為: (1)如果對給定的一個傳遞函式矩陣W(、)，找到 一個狀態空間表達式 x一Ax+Bu y一Cx+刀“ 簡寫為(‘，“，c，”，{(9， 使W(s)寶c(sI一A)一‘B十D成立，則稱(A，B，C，D)為 具有傳遞特性w(s)的系統的一個實現。它本質上是一 個狀態空間領域內的假想結構，與真實系統具有相同 的傳遞特性。 (2)並不是任意給定的w(s)都可以找到其對應的 狀態空間表達式的。要滿足可實現性條件:w(s)的元 素(傳遞函式)w:凡(s)，i一1，2，…，婦泛一1，2，…， p。其分子多項式的次數必須低於或等於分母多項式 的次數。對於定常系統，w茂(:)中分子、分母多項式的 係數均為實常數，-一----一----------一一-一 招)實現不是唯一的，即狀態空間表達式不是唯一 的。它們可以是代數等價的或代數不等價的。 (4)對於給定的w(s)，一定存在一類維數最低的 實現，稱去最小實現。它反映了W(:)的假想結構的最 簡形式。最小實現的充要條件是懷，萬，c，D)為完 全可控和完全可觀測的。最小實現也不是唯一的。不同 的最小實現其維數相同且代數等價。如果真實系統不 是完全可控和可觀測的，最小實現在結構上只是代數 等價於真實系統中可控且可觀測的那一部分。
