簡介
如同隨機變數的統計特性可用它的特徵函式表征那樣,特徵泛函作為特徵函式的推廣形式,能提供隨機過程分布律的一個完全的統計刻畫。因此,特徵泛函是研究隨機過程(特別是隨機點過程)的一種有用的工具。
隨機過程的特徵泛函相應於隨機變數或隨機向量的特徵函式或聯合特徵函式。特徵泛函既等價於整個過程的分布(有限維分布函式族),又能快速的得到一切矩。 廣義隨機過程的特徵泛函的概念是機率分布的特徵函式概念的推廣。
Poisson過程的特徵泛函
定義
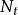 特徵泛函
特徵泛函 特徵泛函
特徵泛函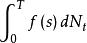 特徵泛函
特徵泛函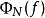 特徵泛函
特徵泛函對於Poisson過程 及定義在[0,T]上的函式 ,我們將 的特徵函式在1處的值記為 ,即
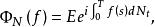 特徵泛函
特徵泛函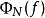 特徵泛函
特徵泛函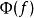 特徵泛函
特徵泛函這裡的f是參變函式,對於給定的一個函式f,就有一個數 與之對應,這種從函式f到 的映射稱為泛函,又因為此泛函是通過Poisson過程的積分生成的,所以稱之為Poisson過程的泛函。
定理
Poisson過程的特徵泛函的表達公式為:
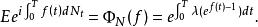 特徵泛函
特徵泛函非時齊的Poisson過程的特徵泛函
定義
非時齊的Poisson過程的特徵泛函仍定義為:
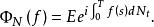 特徵泛函
特徵泛函定理
非時齊的Poisson過程的特徵泛函的表達公式為:
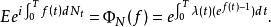 特徵泛函
特徵泛函Gauss過程的特徵泛函
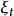 特徵泛函
特徵泛函對於期望函式為0,協方差函式為R(s,t)的Gauss過程 ,及任意連續增函式f(t),定義Gauss過程的特徵泛函為:
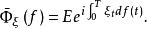 特徵泛函
特徵泛函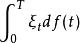 特徵泛函
特徵泛函它是Gauss隨機變數在 的特徵函式在1處的值。

