簡介
在理論物理中, 熱量子場論(簡稱 熱場論) 或 有限溫度場論(finite temperature field theory) 是計算在有限 (不為零的)溫度下,量子場論中物理可觀察量之期望值的方法。
在松原方法(Matsubara formalism) 中,一個運運算元在熱系綜的期望值
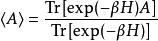 熱量子場論
熱量子場論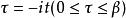 熱量子場論
熱量子場論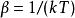 熱量子場論
熱量子場論 熱量子場論
熱量子場論可以被量子場論中以虛數時間所演化的期望值所表示。由於使用虛數時間,計算上可以使用歐幾里得度量的時空。式中的跡 要求所有的玻色場在歐幾里德時間方向τ上皆有周期為的周期性,而費米場則有反周期性。此方法讓我們能夠使用量子場論中已存在的技巧,如泛函積分和費曼圖等,並將其中的時間修改為緊緻的歐幾里德時間來做計算。同時,正規順序 (Normal Ordering) 的定義也必須被修改。在動量空間下,這對應於將原本連續的頻率,以離散的虛數 (松原) 頻率取代。透過德布羅意關係,這對應於離散的熱能量頻譜。這樣的方法被證明對研究量子場論在有限溫度下的現象很有效,並且已經被推廣到規範場論,是研究楊-米爾斯理論中去禁閉 (deconfining) 相變猜想的重要工具。在歐式空間場論中,實數時間下的可觀測量可以由解析延拓獲得。
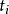 熱量子場論
熱量子場論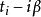 熱量子場論
熱量子場論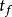 熱量子場論
熱量子場論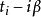 熱量子場論
熱量子場論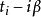 熱量子場論
熱量子場論有限溫度場論,除了使用非真實的虛數時間來計算,還有兩種使用實數時間 (real-time formalism) 的方法。第一種是依路徑排序 (path-ordered) 的實數時間方法,其包含了Schwinger-Keldysh formalism及其他更近代的版本。後者將一條原本從負的(大的)初始時間出發到的直線路徑,取代為一條先經過正的(大的)實數時間 再適當的回到的路徑。事實上,真正需要的是一段經過實數軸的路段,而前往終點所選的路線是較不重要的。這樣以區段 (piecewise) 方式組成的複數時間路徑,造成場的數量增倍以及更複雜的費曼規則,不過卻避免了使用虛數時間方法所需的解析延拓。 另一種實數時間方法稱為熱場力學 (thermo field dynamics),是一種以運運算元為基礎,使用勃格留波夫變換(Bogoliubov transformation) 的方法。就如費曼圖和微擾論等方法一樣,其他技巧如色散關係 (dispersion relations) 和有限溫度的 Cutkosky rules 也都可以在實數時間方法中使用。
另一種在數學物理上感興趣的方法是使用KMS 態來處理。
量子場論
在理論物理學裡, 量子場論(英語: Quantum field theory,簡稱 QFT)是結合了經典場論、狹義相對論和量子力學的一套自洽的概念和工具。在粒子物理學和凝聚態物理學中,量子場論可以分別為亞原子粒子和準粒子建立量子力學模型。量子場論將粒子視為更基礎的場上的激發態,即所謂的量子,而粒子之間的相互作用則是以相應的場之間的互動項來描述。每個相互作用都可以用費曼圖來表示,這些圖不但是一種直觀視化的方法,而且還是相對論性協變攝動理論中用於計算粒子互動過程的一個重要的數學工具。
參閱
•松原頻率
