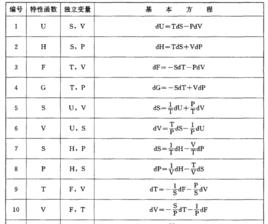
熱力學特性函式及性質
在熱力學中，最基本的是物態方程、內能和熵，其它熱力學函式均可由這3個基本函式導出。由於處於平衡態的系統，其性質由熱力學函式描述，因此，只要知道這3個基本熱力學函式，均勻系統的平衡性質就完全確定了。也就是說，要確定均勻系統的平衡性質一般需要知道3個函式 。
如果由某一函式可導出上述3個基本熱力學函式，這一函式就可以完全確定一個均勻系的平衡性質，表明它是表征均勻系統特性的，那么該函式就被稱為這個系統的特性函式。如果特性函式存在，那么要確定均勻系統的平衡性質只需要知道一個函式就可以了。
熱力學函式獨立變數的選擇有任意性。馬休在 1869 年證明，如果適當選擇獨立變數（稱為自然變數），只要知道一個熱力學函式及它的自然（正則）變數，就可以通過求偏導而求得均勻系的全部熱力學函式，從而把均勻系統的平衡性質完全確定，這個熱力學函式即熱力學特性函式。
例如，對於一個熱力學函式若適當地選擇其獨立變數時，即U(S,V)，H(S,p)，F(T,V)，和C(T,p)就可以用其中任一個狀態函式來導出3個基本熱力學函式，從而推得體系所有其它的熱力學函式（包括U,H,F,S,T,p,V等）。如此選定獨立變數的熱力學函式，因具有以上的特性，故為熱力學特性函式 。
特性函式的套用
證實特性函式的存在是熱力學的重大成就．但由於這些函式的表達式不能從熱力學定律本身得到，使得在熱力學範圍內，仍然沒能充分利用這些成就。然而，由於特性函式本身所具有的性質——由它可以推得體系所有其它的熱力學函式，即它可以直接和其它熱力學函式（或它們的偏導數）聯繫起來，這就決定了套用它會給解決熱力學問題帶來極大的方便 。
在熱力學中，涉及熱力學函式偏導數的恆等式證明題很多，證題的技巧性也很強，但套用特性函式來求證就不需要更多的數學技巧。下面列舉實例具體說明。
焓態方程：
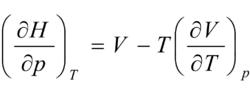熱力學特性函式的導出。
觀察欲證等式，變數為T,p， 如果選擇T,p為獨立變數，C(T,p)為特性函式．由吉布斯函式和焓的定義式，可知 C 與 H 的關係為：
H=C+TS
則：
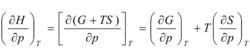熱力學特性函式由熱力學基本方程dC=-SdT+Vdp及麥氏關係，可得焓態方程：
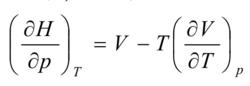熱力學特性函式類似的證明問題在熱力學中還有很多，通常的做法都要利用一些數學關係式，如偏微商的循環關係式和鏈式及倒置式、全微分式及其判別式、雅可比式等來解決，技巧也主要在證明的每一步選擇什麼公式進行變換能使證明最簡單，可以說一題一法，較難掌握 。
