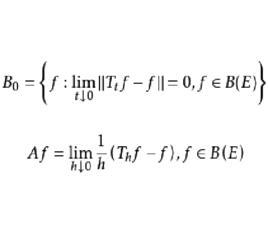基本介紹
無窮小運算元亦稱無窮小生成元,隨機過程理論的重要概念。它可對任意巴拿赫空間上的任一運算元半群來定義。此處是對馬爾可夫半群而言,如果下面二式右端極限按範數意義存在,則記
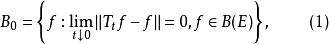 無窮小運算元
無窮小運算元定義運算元A:
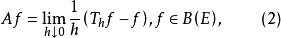 無窮小運算元
無窮小運算元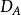 無窮小運算元
無窮小運算元 無窮小運算元
無窮小運算元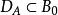 無窮小運算元
無窮小運算元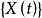 無窮小運算元
無窮小運算元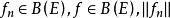 無窮小運算元
無窮小運算元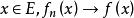 無窮小運算元
無窮小運算元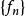 無窮小運算元
無窮小運算元 無窮小運算元
無窮小運算元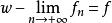 無窮小運算元
無窮小運算元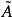 無窮小運算元
無窮小運算元記為的定義域,則有。運算元A稱為馬氏過程的(強)無窮小運算元。若(1),(2)的極限是弱收斂極限(即若有界,且對每一,則稱弱收斂於,記為),並稱相應的運算元為 弱無窮小運算元。無窮小運算元A是線性的,但未必有界 。
馬爾可夫過程的無窮小運算元
定義
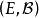 無窮小運算元
無窮小運算元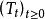 無窮小運算元
無窮小運算元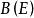 無窮小運算元
無窮小運算元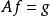 無窮小運算元
無窮小運算元 無窮小運算元
無窮小運算元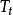 無窮小運算元
無窮小運算元設為某可測空間,為作用於中的壓縮運算元半群。由公式決定的運算元稱為半群的 無窮小運算元(infinitesimal operator),若
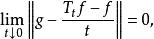 無窮小運算元
無窮小運算元 無窮小運算元
無窮小運算元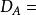 無窮小運算元
無窮小運算元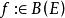 無窮小運算元
無窮小運算元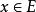 無窮小運算元
無窮小運算元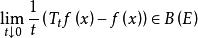 無窮小運算元
無窮小運算元的定義域為{,且對一致存在} 。
無窮小運算元性質
無窮小運算元性質:
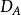 無窮小運算元
無窮小運算元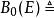 無窮小運算元
無窮小運算元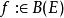 無窮小運算元
無窮小運算元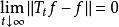 無窮小運算元
無窮小運算元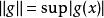 無窮小運算元
無窮小運算元(1) 集依範數收斂(稱強收斂)意義下的閉包與集{且}重合;此處。
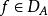 無窮小運算元
無窮小運算元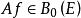 無窮小運算元
無窮小運算元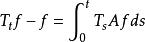 無窮小運算元
無窮小運算元(2) 如,則且;
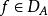 無窮小運算元
無窮小運算元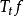 無窮小運算元
無窮小運算元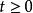 無窮小運算元
無窮小運算元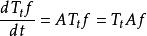 無窮小運算元
無窮小運算元(3) 如,則對強可微,且;這裡強可微是指強收斂意義下可微。
(4) 運算元A封閉 。