無源控制把控制理論的研究架構從傳統的信號處理的角度轉到能量處理(傳輸)的角度,其物理概念非常直觀,易於被工程師接受,目前在諸多實際的物理系統中存在著廣泛的套用。其核心是從能量的角度入手,使得閉環系統滿足無源性。相關的無源控制理論自1989年提出至今的三十年里,取得飛速的發展。
能量觀點
無源控制理論中最核心的是能量的觀點,在此之前控制理論通常是在信號處理的觀點下發展而來的。PBC中將被控對象視作多連線埠的能量傳輸設備,而物理系統滿足如下的(廣義)能量守恆關係:
儲存能量 = 供給能量 + 耗散
PBC的控制目標是維持系統的能量守恆,但是建立如下能量關係:
期望儲存能量 = 新供給能量 + 期望耗散
換而言之,PBC的目標可以總結如下:
PBC = 能量成型 + 阻尼配置
無源化實現方法
對於一般非線性系統而言,目前有三種可行的思路實現無源。
•通過狀態反饋實現無源化或改變系統的能量函式(energy function);
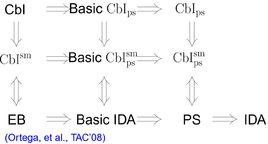
•通過互聯控制(Control by Interconnection, CbI):控制器和被控對象都看作能量傳輸設備,閉環系統的總能量是它們相加在一起;
•將系統分解為無源的(或可無源化的)子系統,對每個子系統分別設計PBC。
PBC優點
PBC方法相對於高增益(high gain)控制器設計思路具有如下優勢:
•可以處理系統的動態性能,而不僅僅只是穩定性;
•從單純研究控制系統結構,擴展到:1)引入物理知識;2)對控制行為提供物理解釋;
•能量是溝通控制理論學者與控制工程師共同的語言;
•對以下兩個問題有著優美的幾何解釋:1)功率守恆互聯(通過Dirac結構);2)對於可無源化的非線性系統(通過穩定可逆性與相對階的概念)
PBC套用對象及場景
過去三十年里,PBC在物理對象的研究主要包括一些方面:
•機械系統:移動機器人、雙邊遙操作機器人、球車系統;
•化學過程:質量平衡系統、庫存控制、反應堆;
•電力系統:電力變換器等;
•機電系統:電機、磁懸浮系統;
•交通系統:水下潛器、水面船舶、空間飛行器;
•網路化控制:編隊控制、同步、一致性問題;
•混雜系統:切換系統、混雜無源化。
關鍵性質:Cyclo-Passivity
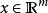 無源控制
無源控制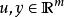 無源控制
無源控制定義:當一個m連線埠系統,其狀態, 功率連線埠變數滿足如下條件
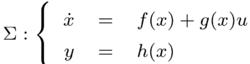 無源控制
無源控制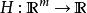 無源控制
無源控制該系統滿足cyclo-passive,如果存在一個儲存能量函式使得
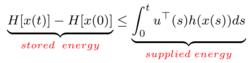 無源控制
無源控制此外,若H(x)>=0,那么該系統是無源的,其連線埠變數為(u,y),儲存能量函式為H(x)。
系統鎮定:能量成型與阻尼注入
當系統輸入u(t)恆為0是,若有如下性質
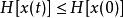 無源控制
無源控制那么系統的軌跡將收斂向能量最低點,若能量最低點是嚴格的,H(x)可以作為分析該系統的Lyapunov函式。
為了改變系統的平衡點到期望的x*,PBC需要對能量進行成型,讓x*成為嚴格的能量最低點。
進一步地,若我們在連線埠引入
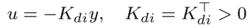 無源控制
無源控制那么我們可以得到
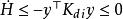 無源控制
無源控制這樣若h(x)是對閉環系統是可檢測的,x(t)將會收斂到0。以上為能量成型與阻尼注入的基本思路。
該思路可以克服分析系統結構採用高增益(主導思想)帶來的一些弊端,目前的主要難點來源於偏微分方程(PDE)的可解性與方程求解。