簡介
在物理學中, 潛能是物體由於相對於其他物體的位置、自身內部的應力、電荷或其他因素而所擁有的能量。常見類型的潛內能包括:取決於其的物體質量與質量中心距離的的重力勢能,彈簧的彈性勢能,電荷在電場電勢能,能量在國際單位制(SI)中的單位是焦耳,其符號為J。
潛能一般會用單位質量或是單位莫耳下的能量來表示,例如J/mol或BTU/lb。正號表示能量加入系統中,負號表示從系統中移出能量。每一種潛能都有一與其數值相同,但符號相反的潛能,例如熔化(固態變為液態)的潛內能數值就和凝固(液態變為固態)的潛能數值相同,但符號相反。
歷史
潛能一詞由19世紀的蘇格蘭工程師和物理學家威廉·蘭金(William Rankine)引入,儘管它與希臘哲學家亞里士多德的潛力概念有關。 潛能與作用於物體的力相關聯,使得這些力在身體上完成的總工作僅取決於身體在太空中的初始和最終位置。 這些被稱為保守力的力可以通過表示為稱為勢的某個標量函式的梯度向量在空間中的每個點處表示。
定義與計算
 潛內能
潛內能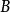 潛內能
潛內能 潛內能
潛內能潛能與力量密切相關。如果一個力從 移動到 的物體所做的功不依賴於這些點之間的路徑(如果工作是由保守力完成的)那么從 測量的這個力的工作會給出一個標量值到空間中的每個其他點並定義一個標量勢場。在這種情況下,力可以定義為勢場的矢量梯度的負值。
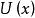 潛內能
潛內能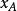 潛內能
潛內能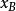 潛內能
潛內能如果施加力的作用與路徑無關,那么力的作用將在套用點的軌跡的開始和結束處進行評估。這意味著存在稱為“勢”的函式 ,其可以在兩個點 和 處進行評估,以獲得在這兩個點之間的任何軌跡上的工作。傳統的做法是用負號來定義這個函式,這樣積極的工作就是減少潛力,即
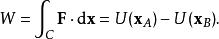 潛內能
潛內能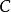 潛內能
潛內能 潛內能
潛內能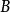 潛內能
潛內能 潛內能
潛內能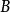 潛內能
潛內能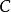 潛內能
潛內能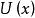 潛內能
潛內能其中 是從 到 的軌跡。因為完成的工作與所採用的路徑無關,所以對於從 到 的任何軌跡 ,該表達式都是正確的。函式 被稱為與施加的力相關聯的勢能。具有潛能的力的示例是重力和彈簧力。
功與潛能
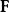 潛內能
潛內能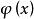 潛內能
潛內能下面介紹功與潛能之間的關係。如果力 與標量場 相關,
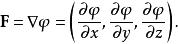 潛內能
潛內能則沿曲線定義功的線積分採用特殊形式,沿曲線的功由下式給出
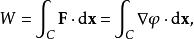 潛內能
潛內能可用梯度定理來評估得到
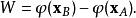 潛內能
潛內能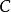 潛內能
潛內能 潛內能
潛內能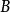 潛內能
潛內能 潛內能
潛內能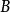 潛內能
潛內能這表明當力可以從標量場導出時,沿曲線 的那些力的功是通過評估曲線的起點 和終點 處的標量場來計算的。這意味著功積分不依賴於 和 之間的路徑,即與路徑無關。
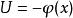 潛內能
潛內能勢能 傳統上被定義為該標量場的負值,因此力場的功減少了勢能,即
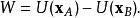 潛內能
潛內能 潛內能
潛內能在這種情況下, 運算符套用於功函式,
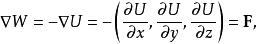 潛內能
潛內能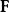 潛內能
潛內能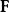 潛內能
潛內能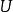 潛內能
潛內能 潛內能
潛內能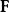 潛內能
潛內能且力 可從勢中導出。這也必然意味著 必須是保守的向量場。潛能 在空間中的每個點 處定義力 ,因此該組力被稱為力場。
潛能計算
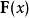 潛內能
潛內能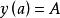 潛內能
潛內能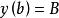 潛內能
潛內能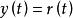 潛內能
潛內能給定力場 ,使用梯度定理對功積分的評估可用於找到與勢能相關聯的標量函式,可通過從 到 引入參數化曲線 來完成的,計算如下:
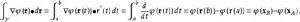 潛內能
潛內能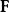 潛內能
潛內能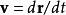 潛內能
潛內能對於力場 ,設 v= d r/ dt,然後梯度定理得到,
 潛內能
潛內能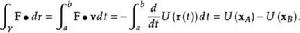 潛內能
潛內能通過力場施加到身體的功率是從施加點的速度的方向上的功或電勢能的梯度獲得的,即,
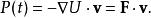 潛內能
潛內能可以從潛能計算功的示例是重力和彈簧力。
