說法
滾動阻力
首先,我們來看一下物體的滾動。以正方體為例,如圖1所示,設重力為G,重心到瞬心O的距離為 e,在外力 P作用下發生滾動。顯然,G·e是滾動的阻力。
隨著物體的滾動,e 逐漸縮小;G·e 也隨著一同減小。當G與N共線時 G·e 為零,越過共線點,-e的絕對值逐漸增大,Ⅰ- G·eⅠ 也隨著一同增大;此時無須外力 P作用,物體便能自行滾動至穩態。我們把阻力矩從最大值 G·e 到最大值Ⅰ- G·eⅠ 稱為一個力矩周期。在這個周期內,G·e 由最大阻礙作用變為最大動力作用,折而重新為阻力,開始下一個力矩周期。
 滾動摩擦力
滾動摩擦力圖1-正方體的滾動過程
這種由物體重力引起的滑動阻礙作用和滾動阻礙作用大小的比較來看,多數場合滾動阻礙作用要顯得大些, 但圓形體的滾動阻礙作用卻很小。這是因為圓形體特有的幾何形狀所造成的。通常我們講的滾動多是指圓形體的滾動。下邊我們看一下圓形體的滾阻力矩:
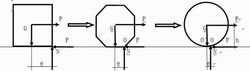
如圖2所示,如果增加正方體的棱邊我們會發現 ,e隨著棱邊個數n的增加而減小,從而導致G·e的初始值減小,力矩變化周期也隨之縮短。當n趨於無窮大時,這個正多稜體趨於圓。此時,由於圓周上各點到圓心的距離相等,-e現象消失;力矩G·e趨於一常量,並且,在滾動中始終維持在滾動前的臨界狀態。這個常量就是圓形體的滾動阻力。比較起來,這個圓形體G·e的阻礙作用要比滑動時由摩擦引起的阻礙作用小得多。
人的行走就相當於多邊形體的滾動,步幅的一半相當於力臂e。
 滾動摩擦力
滾動摩擦力圖 2-棱邊個數n增加對e的影響
力矩N·e不是摩擦作用
通常,對滾動分析都是採用如圖6中圓形體的形式進行的。圖中G為物重;P為外力;F為摩擦力;N為G的反作用力;e為外力作用下N的偏移量;O′為N的原始作用點;O為瞬心;h為外力P到瞬心的距離。這裡需要特別注意的是瞬心的確定。在我們的教材和有關書籍中多是以轉動體的質心或O′點為平衡中心來進行滾動分析的。實際上,這些點臨界時為動點,不能直觀地顯示出物體的臨界運動狀態,容易造成分析上的錯誤;而O點為滾動體的臨界力矩中心,是瞬時不動點。因此,我認為選擇O點作為平衡中心來進行分析較為恰當。
從圖中我們可以看出,主動力P能使物體繞O點轉動,即滾動。這種滾動是轉動的一種特殊運動狀態,它是轉動中心不斷改變的一種力矩效應,距心即是瞬心。在滾動過程中由於瞬心O的位置沿貼切面不斷改變,從而使兩物體產生了相對運動。此時N、F對O點的矩均為零。因此,它們既不是滾動的動力,也不是滾動的阻力。只有G對O點的距與主動力矩相反。所以,它才是滾動的阻力。
以往,我們多是採用力偶M(G,N)或力矩N·e的形式來解析滾動阻力,並稱之為“摩擦作用”。從數學算式來看,它們與G·e是等量的,但從物理作用來講,它們是有區別的。從前邊的分析中我們可以看出,滾動的阻力實質上是因物體位移產生的反作用,一般用G·e表示較為恰當。即使是採用M(G,N)或N·e的形式,將其作為摩擦作用來解釋也是不正確的。而N與G在豎直方向平衡,故N並不隨外力P的改變而變化。當外力P去除時N仍存在,而對摩擦作用來講,當外力去除時是不存在的,這是N與摩擦力的本質區別;同樣,力臂 e也不具備摩擦特徵,它是由物體的剛度、物重、材質和幾何形狀等因素確定的,並不受滾動力矩大小的影響。因此,不能把N·e視為“摩擦作用”。
摩擦的輔助作用
力偶和力矩都能使物體滾動,但它們對瞬心有平動作用。滾動時的摩擦作用就是這種平動作用引起的反作用. 它和具有滑動趨勢時的摩擦作用是一樣的,也是靜摩擦力.
這個反作用力F的大小對物體的滾動有很大影響。以往的討論都是假定F大於P(或Pm)的條件下進行的,當F小於P(或Pm)時,物體將產生滑動或轉動,這類事實在我們日常生活中是常見的。例如,若腳下很滑(即摩擦作用小),人行走就會很吃力;汽車若在帶凍的路上行駛會出現‘打滑’。它們都說明摩擦對滾動運動有很大影響。也就是說,對滾動來講, 摩擦作用是穩定瞬心,使之不產生位移的必要條件。摩擦作用越大,瞬心穩定性越強;沒有摩擦作用就不能產生滾動。
力偶和力矩對瞬心的平動作用方向不同。力矩對作用點的平動作用需要用反向作用力來平衡,而力偶對作用點的平動作用需要用與力偶中另一力同向的作用力來平衡。腳踏車前、後輪摩擦力方向不同就是這個原因。由此得出,滾動體的瞬心受力偶作用時,摩擦力方向與滾動體運動方向相同,受力距作用時,與滾動體運動方向相反;反之,此推論也成立.例如人行走時摩擦力方向向前,故人的行走(滾動)動力是力偶作用;若是被人推著走則磨擦力方向向後,則是力矩作用.
以上還說明,無論是滑動時的摩擦還是滾動時的摩擦,都是平動的阻力,只不過對兩種運動所表現的作用不同而已,一個表現為阻抗性,一個表現為輔助性。因此,我們不應把摩擦分為兩類。
