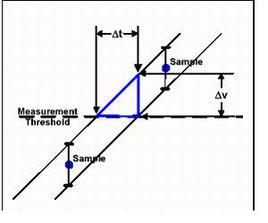
定義
測量不確定度是指測量結果含有的一個參數,用以“表征合理地賦予被測量之值的分散性” 。
來源
實際工作中不確定度的來源一般有以下幾點 :
被測量定義不完善
測量樣本不能完全代表定義的被測量
被測量定義實現不理想
測量人員
環境
參數不準
測量儀器
測量方法和程式的近似和假設
在相同的測量下,重複測量中的隨機變化
測量列中的粗大誤差因不明顯而未被剔除
1.被測量定義不完善
2.測量樣本不能完全代表定義的被測量
3.被測量定義實現不理想
4.測量人員
5.環境
6.參數不準
7.測量儀器
8.測量方法和程式的近似和假設
9.在相同的測量下,重複測量中的隨機變化
10.測量列中的粗大誤差因不明顯而未被剔除
A類評定
貝塞爾法
 測量不確定性
測量不確定性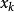 測量不確定性
測量不確定性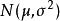 測量不確定性
測量不確定性對於某量 進行多次獨立測量,得到測量列的分分布滿足常態分配 ~ ,則單次測量的標準差估計為
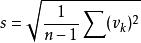 測量不確定性
測量不確定性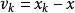 測量不確定性
測量不確定性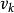 測量不確定性
測量不確定性式中 , 稱為殘差。該式稱為貝塞爾公式,由貝塞爾在研究儀器誤差理論時得到 。
最大殘差法
設測量測服從常態分配,則由最大殘差得到標準差的估計為
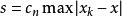 測量不確定性
測量不確定性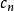 測量不確定性
測量不確定性的取值見下表,該方法由中國計量科學研究院劉志敏研究員於1979年提出 。
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 |
| c | - | 1.77 | 1.02 | 0.83 | 0.74 | 0.68 | 0.64 | 0.61 | 0.59 | 0.57 | 0.51 | 0.48 |
彼得斯法
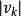 測量不確定性
測量不確定性 測量不確定性
測量不確定性俄羅斯天文學家彼得斯採用 計算 減弱了粗大誤差值的影響 。
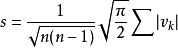 測量不確定性
測量不確定性其他方法
其他方法還有極差法、最大誤差法等
B類評定
B類評定方法有別於統計分析法,是基於其他方法估計機率分布或假設服從某種分布評定標準不確定度的。關於B類評定主要是通過一定的實驗,對測量列進行統計分析,以標準差表征其量值,其可靠性不僅與重複測量的次數有關,還與機率分布的類型有關。合理使用B類不確定度要求對經驗及相關知識有透徹的了解,一般靠長期的實驗經驗逐步累積 。
倍數法
如x取自製造說明書、校準證書、手冊或其他來源,且給出的不確定度U(x)為標準差的k倍,則標準不確定度 :
常態分配法
當估計值x受到多個獨立因素的影響且影響的大小相近,可假設其服從常態分配
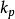 測量不確定性
測量不確定性 測量不確定性
測量不確定性1)若給出的不確定度U(x)對應的置信水準為90%、95%、99%、99.97%,可將不確定度除以適當的因子 ( ),即可得到標準不確定度
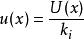 測量不確定性
測量不確定性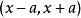 測量不確定性
測量不確定性2)當x落入內的機率為50%,可取
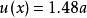 測量不確定性
測量不確定性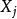 測量不確定性
測量不確定性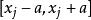 測量不確定性
測量不確定性3)當在的機率為0.68,則
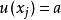 測量不確定性
測量不確定性均勻分布法
當X在[x-a,x+a]內各處出現的機會相等而區間外不出現時,X服從均勻分布,其最佳值x的標準不確定度為 :
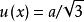 測量不確定性
測量不確定性反正弦分布法
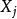 測量不確定性
測量不確定性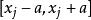 測量不確定性
測量不確定性 測量不確定性
測量不確定性當受到均勻分布的正餘弦函式影響,它服從的反正弦分布,則最佳值的標準不確定度 :
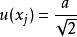 測量不確定性
測量不確定性其他方法
其他方法還有梯形分布與三角分布法、投影分布法等
測量不確定度的合成
合成標準不確定度的計算公式
 測量不確定性
測量不確定性當測量結果受各種因素的影響而具有若干個不確定度分量時,測量結果的標準不確定度可用各標準不確定度的分量通過合成得到,一般用 表示:
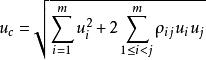 測量不確定性
測量不確定性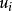 測量不確定性
測量不確定性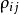 測量不確定性
測量不確定性為第i個標準不確定度分量; 為第i個和第j個標準不確定度分量之間的相關係數;m為不確定度分量的個數 。
間接測量中不確定度的合成公式
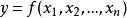 測量不確定性
測量不確定性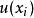 測量不確定性
測量不確定性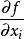 測量不確定性
測量不確定性在間接測量中,被測量Y的估計值y是由N個其他直接測量的測得值的函式求得的, 。若已知各直接測得值x的測量標準不確定度為 ,它對被測量估計值影響的傳遞函式為 ,則由x_i引起被測量y的標準不確定度分量為 :
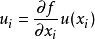 測量不確定性
測量不確定性測量結果y的不確定度的計算公式為:
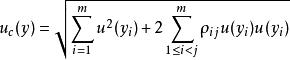 測量不確定性
測量不確定性 測量不確定性
測量不確定性 測量不確定性
測量不確定性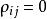 測量不確定性
測量不確定性當 和 相互獨立獨立時,即 ,合成公式可以簡化為:
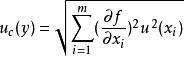 測量不確定性
測量不確定性