方程
實際中液壓油總是在流動的，因此除了研究靜止液體的性質外，還必須研究液體運動時的現象和規律，液體流動時的三個基本方程，即連續性方程、伯努利方程、動量方程。
基本概念
理想液體和穩定流動
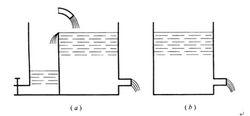穩定流動和不穩定流動，因此在研究流動液體時必須考慮黏性的影響。為了分析問題簡便，通常先假設液體沒有黏性，推導出一些理想的簡單結論，而黏性的影響則通過實驗對理想的結論加以修正。對於液體的可壓縮性問題，也可用同樣方法處理。
（1）理想液體
在研究流動液體時，將假設的既無黏性又無壓縮性的液體稱為理想液體，而事實上存在的有黏性和可壓縮性的液體稱為實際液體。
（2）穩定流動
液體流動時，若液體中任一點的壓力、速度和密度都不隨時間而變化，則這種的流動稱為穩定流動。若在壓力、速度和密度中有一個量隨時間變化，就稱為不穩定流動。圖a為穩定流動，圖b為不穩定流動。穩定流動與時間無關，研究比較方便，而不穩定流動研究起來比較複雜。因此在研究液壓系統的靜態性能時，往往將一些不穩定流動問題適當簡化，作為穩定流動來處理。
流量和平均流速
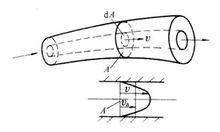流量和平均流速流量和平均流速是描述液體流動的兩個主要參數。液體在管道中流動時，通常將垂直於液體流動方向的截面積稱為通流截面。
單位時間內通過某過流斷面的液體的體積稱為流量。一般用符號q表示。常用法定計量單位有m3/s或L/min等，單位的換算關係為： 1m3/s=6×104L/min=1×106ml/s
在實際中，由於液體在管道中流動時的速度分布規律為拋物面，計算較為困難。為了便於計算，現假設過流斷面上流速是均勻分布的，且以均布流速va流動，流過斷面A的流量等於液體實際流過該斷面的流量。流速va稱為流斷面上的平均流速，以後所指的流速，除特別指出外，均按平均流速來處理。於是有q=vaA，故平均流速va為 va=q/A
在液壓缸中，液體的流速與活塞的運動速度相同，由此可見，當液壓缸的有效面積一定時，活塞運動速度的大小，由輸入液壓缸的流量來決定。
液體的流動狀態
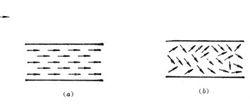層流和紊流英國物理學家雷諾通過大量的實驗，發現了液體在管路中流動時有層流和紊流（也稱湍流）兩種流動狀態，在層流時，液體質點沿管路做直線運動，互不干擾，沒有橫向運動，即液體作分層流動，各層間的液體互不混雜。在紊流時，液體質點除了沿管路運動外，還有橫向運動，呈紊亂混雜狀態。實驗證明，圓管中液體的流動狀態與液體的流速 v、管路的內徑 d以及油液的運動黏度 ν有關。因此能判定液體流動狀態的則是這三個參數所組成的一個無量綱的雷諾數 Re，即 Re=vd/ν
雷諾數的物理意義；雷諾數是液流的慣性力與內摩擦力的比值。雷諾數較小時，液體的內摩擦力起主導作用，液體質點運動受黏性約束而不會隨意運動，液流狀態為層流；雷諾數較大時，慣性力起主導作用，液體黏性不能約束質點運動，液流狀態為紊流。
實驗指出：液流從層流變為紊流時的雷諾數大於由紊流變為層流時的雷諾數，工程中一般都以後者為判斷液流狀態的依據，稱其為臨界雷諾數，記做 Rec。當 Re< Rec時液流為層流；反之，則多為紊流。
臨界雷諾數由實驗求得。對於光滑金屬圓管中液流的 Rec為2000~2320，對於橡膠軟管液流 Rec的為1600~2000，其他通道的 Rec可查有關資料。
對於非圓形截面的通道，液流的雷諾數可按下式計算： Re=4vR/ν
式中： R為通流截面的水力半徑。
水力半徑是等於液流的有效截面積和它的濕周(過流斷面上與液體接觸的固體壁面的周長) x之比，
即R=A/x
水力半徑的大小對通流能力影響很大。水力半徑大意味著液流和管壁的接觸周長相對較短，管壁對液流的阻力較小，通流能力較大，即使通流截面面積較小也不易堵塞。
詳細內容
連續性方程
連續性方程是質量守恆定律在流體力學中的一種表達形式。
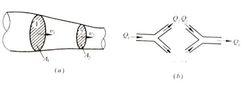液體流動的連續性液體的可壓縮性很小，在一般情況下認為是不可壓縮的，即密度 ρ為常數。由質量守恆定律可知，理想液體在通道中作穩定流動時，液體的質量既不會增多，也不會減少，因此在單位時間內流過通道任一通流截面的液體質量一定是相等的。如左所示，管路的兩個通流面積分別為 A1、A2，液體流速分別為 v1、v2，液體的密度 ρ為，則有
ρv1 A1=ρv2 A2=常量
v1 A1=v2 A2=q=常量 （1-1）
式（1-1）稱為液流的連續性方程，它說明不可壓縮液體在通道中穩定流動時，流過各截面的流量相等，而流速和通流截面面積成反比。因此，流量一定時，管路細的地方流速大，管路粗的地方流速小。
在具有分支的管路中，有Q1=Q2+Q3的關係。
伯努利方程
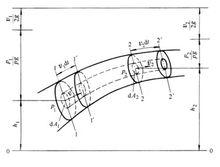伯努利方程示意圖伯努利方程是能量守恆定律在流動液體中的表現形式。為了討論問題方便，我們先討論理想液體的流動情況，然後再擴展到實際液體的流動情況。
1、理想液體的伯努利方程
理想液體在管內穩定流動時沒有能量損失。在流動過程中，由於它具有一定的速度，所以除了具有位置勢能和壓力能外，還具有動能。如圖2-13所示，取該管上的任意兩截面1-1和2-2，假定截面積分別為 A1、 A2，兩截面上液體的壓力分別為p1、p2速度分別為v1和v2，由兩截面至水平參考面的距離分別為h1、h2。根據能量守恆定律，重力作用下的理想液體在通道內穩定流動時的伯努利方程為
p1+1/2ρv1^2+ρgh1=p2+1/2ρv2^2+ρgh2
或 p+ρgh+(1/2)*ρv^2=常量 （1-2）
式中 p為單位體積液體的壓力能； 為單位體積液體相對乾水平參考面的位能 ；ρv2/2為單位體積液體的動能。
式（1-2）即為理想液體的伯努利方程，它表明了流動液體各質點的位置、壓力和速度之間的關係。其物理意義為：在管內做穩定流動的理想液體具有動能、位置勢能和壓力能三種能量，在任一截面上的這三種能量都可以互相轉換，但其和都保持不變。由此可見，靜壓力基本方程是伯努利方程（流速為零）的特例。
2、實際液體的伯努利方程
式（1-2）是理想液體的伯努利方程，但實際液體具有黏性，在過流斷面上各點的速度是不同的，所以方程中 ρv×v/2這一項要進行修正，其修正係數為 a，稱為動能修正係數。一般液體處於層流流動時取 a=2，液體處於紊流流動時，取 a=1。另外，由於液體有黏性，會產生內摩擦力，因而造成能量損失。若單位質量的實際液體從一個截面流到另一截面的能量損失用 Δ pw表示，則實際液體的伯努利方程為
p1+1/2ρα1v1^2+ρgh1=p2+1/2ρα2v2^2+ρgh2+Δpw
動量方程
動量方程是動量定理在流體力學中的套用。由動量定理可知：作用在物體上的外力等於物體在受力方向上的動量變化率，即 ΣF=mv2/Δt-mv1/Δt
對於在管道內作穩定流動的液體，若忽略其可壓縮性，可將m= ρqΔt代入上式。考慮到以平均流速代替實際流速會產生誤差，因而引入動量修正係數 β，則上式變成
ΣF=ρqv2-ρqv1=ρqβ2va2-ρqβ1va1
上式為流動液體的動量方程（矢量方程）。當液流為紊流時取 β=1，為層流時取 β=1 .33。
