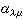建立液滴模型時有兩個主要的事實依據
一個是原子核每核子的平均結合能幾乎是常數,即結合能正比於核子數,顯示了核力的飽和性(見核力);另一個是原子核的體積正比於核子數,即核物質的密度近似是個常數(見原子核),顯示了原子核基本上是不可壓縮的。通過同液體類比,
包含內容
液滴模型主要包括以下幾個方面。
球形核的表面振動
一個半徑為R0的球形液滴,當它發生形變時,在球坐標中,其表面曲率半徑R(θ,嗞)可用參量來表示 (1)
式中Y(θ,嗞)為球諧函式,μ從-λ到λ。
在初級近似下,可以不考慮可壓縮性。因此,N可取為保持體積不變的因子: (2)
準確到二級近似,表面振動的動能、勢能分別表示為 其中為恢復力參量,為質量參量。而表面振動能為 (3)
在常密度理想流體的非鏇流動的情況下, (4)
。 (5)
式中ρ是質量密度,而 (6)
同液滴的表面能相聯繫,S為表面張力係數,b1=4πr娿S≈17MeV,r0=1.24fm, (7)
同液滴的庫侖能相聯繫,Z為核電荷數,e為電子電荷。
所以,液滴模型下的振動圓頻率為 (8)
同原子核中實際存在的振動模式相比,公式(8)給的值偏大,而且不能給出實驗值所表現出的殼效應。
核裂變機制
1939年,N.玻爾和J.A.惠勒基於液滴模型提出的一種核裂變機制,以後又有進一步的發展。
由式(3)可知,隨著形變參量的變化,原子核(帶電的液滴)的勢能將隨之發生變化。如僅考慮λ=2的小形變,則勢能為 (9)
顯然,當C2>0時,球形液滴是穩定的,而當C2<0時,球形液滴不穩定,會發生大形變以至裂變。
由式(6)、(7)可得球形液滴的穩定條件為 。 (10)
液滴模型還預期,在大形變時,有利於庫侖排斥的長程性質,所以,儘管一些核滿足條件(10),但在大形變時,仍可能是不穩定的。
下頁圖表示了液滴發生裂變時鞍點表面形狀(見核裂變)。x稱為可裂變度參量,用來衡量核發生裂變的難易程度。其定義為 (11)
λ=2時,x=C2/C2。很明顯,x≥1的核因對裂變不穩定而不能存在。
半經驗的質量公式和原子核結合能 原子核的質量mN可表為 (12)
其中A為該核的結合能,N為中子數,mn為中子質量,m為質子質量,с為真空中的光速。基於液滴模型,可以得到結合能中的三項。
①體積能。由於核密度具有飽和性,即核中心密度在原子量A塼20以後近似保持不變,因此,可以期望結合能中主要項為體積能b2A。
②表面能。由於表面核子受到周圍核子的吸引比內部核子所受到的吸引小,所以對體積能應有一修正,它應正比於表面面積4πR娿=4πr娿A,因此,結合能應包含表面能項-b1A。
③庫侖能。均勻的帶電液滴必具有庫侖能。它對結合能的貢獻為-3(Ze)/5R0。
然而,原子核結合能中還有一些內容是液滴模型所不能給出的,它們是:
④對稱能。這一能量來源於原子核有N≈Z的趨勢。從原則上講,它是泡利不相容原理及核力性質的結果,偏離N≈Z的首要項可表為
⑤對能。在原子核中,偶偶核特別穩定,而穩定的奇奇核極為稀少。原子核質量有明顯的奇偶差,原子核內,核子有成對的傾向。所以在結合能中必須包含對能項。而
於是,原子核的質量公式可表為 (13)
公式中的係數可由各種模型導出,但考慮到原子核的複雜性,通常由它與實驗的質量值的擬合來定出,其值為
b2=15.56MeV,b1=17.23MeV,
b3=46.57MeV,b4=12MeV,
r0=1.24fm, ε=0.5。
半經驗的質量公式的形式因導出方法而有所不同。更為普遍的半經驗的質量公式,還要考慮殼層修正、原子核形變及一些高級項。
關於由早期的液滴模型發展到包含幾個非理想流體的液滴模型,並套用於巨共振的內容見巨多極共振。