背景
我國建築抗震設計規範(GBJ11-89)以及剛修訂的抗震設計規範GB50011-2016都建議採用SPT簡化方法,北美、歐洲等則大都採用基於CPT的簡化評價體系。由於多次地震實測資料積累了大量SPT數據,基於SPT的液化簡便評價方法目前仍然是一種較為可靠的方法。Seed提出的液化評價簡化方法已成為北美、歐洲液化評價方法的範式。多年以來,國內不少學者探討了液化判別的機率方法,但對液化勢或液化危害性機率評價則少有涉足。由於以下幾個方面的原因,建立場地液化勢評價機率模型顯得尤為必要。第一,土是一種強非均質性的材料,其材料屬性大都應作為隨機變數或空間隨機變數處理。第二,所謂的液化指數僅表明液化發生後液化效應大小,不能反映液化的可能性。第三,隨著抗震設計理論的發展,基礎設計、上部結構設計都以機率為設計準則,顯然在地基方面仍然採用確定性方法不能使結構設計統一在一個原則上,即都以機率為設計準則。
基於世界範圍內多次地震特別是近幾年發生的幾次大地震實測資料,利用人工神經網路(ANN)模型來搜尋SPT與抗液化能力之間的非線性關係(液化極限狀態方程)。利用機率理論建立液化評價機率模型,在此基礎之上,提出了與我國規範相適應的液化嚴重指數概念和與此相適應的液化勢(液化危害性)分級建議。
理論基礎
最最佳化理論是套用數學的一個重要分支,廣泛套用於各行業的系統管理、設計和決策。最最佳化(optimization)一般是指在某種狀況下作出最好的決策或從幾個候選方案中選出最佳的,其中適於非光滑及導數表達式複雜或寫不出等情形的最佳化搜尋法,是通過試取點函式值的比較來使包含極值的搜尋區間縮小,並當其縮至一定程度時,區間上各點都接近所需要求的極值,則可看作極值的近似,其有黃金分割優選法和Fibonacci最最佳化法(Fibonaccioptimizationmethod,縮寫FOM)。
Fibonacci最最佳化法是Kierer於1953年提出的,又稱分數法,其是基於Fibonacci數列選擇試取點的最佳化搜尋法。
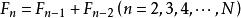 液化勢評價
液化勢評價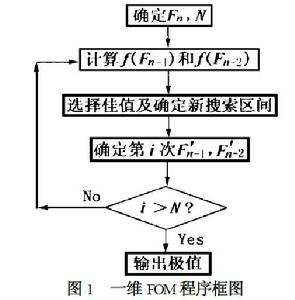 液化勢評價
液化勢評價其中F=1,F=1。若所有可能試驗總數為某個F,先選取F,F兩點作為試取點並比較結果,如果第F點好,則捨去第F點以下的試驗範圍;若第F點好,則划去第F點以上試驗範圍,故新試驗範圍內還剩下F-1個試驗點。重新編號後,第F′或第F′是上步留下的好點,另一個是新試驗點,比較結果並作同上選擇。重複以上步驟直至試驗範圍內沒有該選的點。
若所有可能試驗總數大於某一個F而小於F-1,則先虛設幾個試驗點,湊成F-1個試驗點即可化為前種情況,且設虛設點的試驗結果比其它試取點效果差,可見增加虛設點並未增加試驗次數。圖1給出了求解一維函式f(x),極值在{1,2,3,⋯,M}整數集中的FOM程式框圖。
評價指標
理論研究和實地調查表明地震砂土液化受諸多因素控制,如砂土的平均粒徑和相對密度、地下水水位、地震級數及持續時間等,且每個因素的影響水平是不同的。現場易於獲取的、可靠的主要因素為評價指標,即地震級數M、地面水平加速度a、粘粒含量F、平均粒徑D50、上覆垂直有效應力σ′、實測標貫擊數(SPT)N。
評價模型
前人研究表明砂土液化勢指數是基於經驗的液化靈敏度指數,即是各影響因素的線性或非線性函式,則砂土液化的評價可看作一個多元函式最小值的最最佳化問題,並用多因素的FOM法來求解,即:
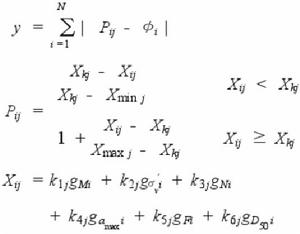 液化勢評價
液化勢評價式中 y為目標函式;P為砂土液化預測值;φ為砂土是否液化實際值;X為最佳化搜尋值;k,k,k,k,k,k為{1,2,3,⋯,N}正整數集合中的點;g,g,g,g,g,g為評價點的M,a,σ′,D,F,N經數據預處理後的數值。
液化極限狀態方程
Juang與前人所用統計分析方法不同,而是基於多次地震場地液化性狀實例採用非線性映射能力強的BP神經網路建立預測模型,通過搜尋算法來建立標貫擊數與抗液化能力之間的非線性關係(液化極限狀態方程)。然而,液化性狀實例庫中沒有將中國幾次主要地震蒐集在內。此外Juang建議的搜尋算法並不一定得到理想的結果。在該液化性狀實例庫基礎上添加了中國包括通海、海城和唐山幾次大地震場地液化性狀實測資料,共297個場地液化實測資料,其中液化184個,非液化場地113個。對於SPT標貫擊數,由於桿長,能量比,細粒含量對其都有一定影響,所以對實測的標貫擊數一般應進行修正。Seed曾說明中國標貫試驗的能量比接近60%,故不進行能量修正。其它諸如桿長等修正項本文由於資料不全而不予考慮。對於細粒含量採用Idriss所建立的方法,即方程(N),=α+β(N)對SPT實測值進行轉換。地震的循環應力比可由Seed建議的經驗公式進行計算:
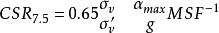 液化勢評價
液化勢評價式中:MSF=(M/7.5);α=峰值加速度;σ、σ′分別為總應力和有效應力;M為矩震級。
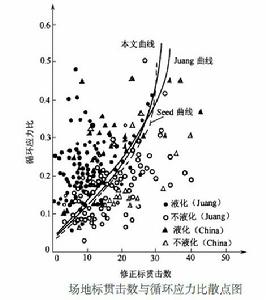 液化勢評價
液化勢評價右圖為297 個場地液化實測數據計算出的修正標貫值與循環應力比(CRR715 ) 散點圖。從圖中可以看出, 液化與不液化點可用圖中的實曲線來區分, 該曲線Juang 稱為液化極限狀態方程。
採用徑向基網路算法, 來搜尋液化與非液化分界點。徑向基函式(RBF) 是一種典型的局部逼近網路, 在逼近能力、分類能力等方面均優於BP 網路。
網路訓練及測試結果表明徑向基網路適用於非線性分類問題。平均判別成功率大於93 %。利用訓練好的網路, 對每一個樣本進行測試, 若液化則減小循環應力比直至輸出結果為非液化; 反之, 則增加循環應力比直至輸出結果為液化。將所有樣本液化性質轉變點的標貫擊數和循環應力比進行曲線擬合。