流態化焙燒 將所處理的固體破碎、研磨成細粉,增加固體與氣體的接觸面積,縮短顆粒內部的傳遞和反應距離。自下而上流經這些粉料的氣體,在達到一定速度時,會將固體顆粒懸浮起來,使之不斷運動,猶如流體,故稱流態化。此項技術已廣泛用於化工、冶金等領域。
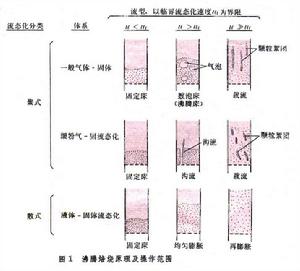
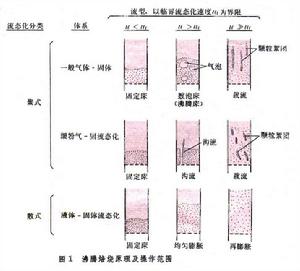
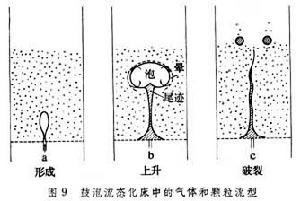
正文 在圖1中用uf來表示臨界流態化速度 。若將流速u增至超過臨界值,即u>uf,一部分氣體會形成氣泡,使整個料層具有沸騰著的液體的狀態,採用這種氣體-固體接觸的焙燒方法叫做流態化焙燒又稱沸騰焙燒。上升氣泡的尾跡中裹有一部分固體顆粒,隨之夾帶而上,使上下的物料混合,有利於整個料層溫度的均勻化,如此,可避免其他常用設備中的不利現象:部分地區因溫度偏低,反應不足;部分地區因溫度偏高,易引起燒結等。若再進一步增加流速,氣泡增多、加大,逐步匯合成一連續氣固混合相;而另一部分顆粒卻團聚為時而形成、時而解體的絮狀體,如此,再次強化顆粒與氣體之間的接觸。但是,不是所有的物料在達到臨界流速 uf後都進入沸騰狀態。有些易於相互粘附、流動性不好的顆粒,特別是較細的粉末,在流速達到臨界值後,會形成溝渠,使部分氣體短路流出,減弱氣、固之間的接觸。對這種內聚性強的物料,只有當流速很大時才形成顆粒團絮的第二種流 型。上述的流型,總稱為聚式流態化:氣體匯聚成氣泡,顆粒匯聚成絮團。與這些不同的是顆粒物料在液體中的流態化。在液-固體系中,隨著流速的增加,顆粒相互離散而單獨運動,不具什麼明顯的泡和團的現象。這種流態化稱為散式流態化,如圖1的下方所示。 流態化焙燒 工藝 流態化焙燒已廣泛用於礦冶工業,具有多種形式。空氣焙燒黃鐵礦是一個放熱反應,採用如圖2的裝置,使冷空氣通過一個多孔板將焙燒著的黃鐵礦粉料噴吹至沸騰狀態,與氧反應生成二氧化硫。一般流態化焙燒爐中需設水冷管或水冷箱,除去多餘的熱量。 流態化焙燒 焙燒反應 器的高溫氫氣提供。為了提高氫的利用率,採用多層床流態化焙燒反應器,使最下層排出來的氣體與上段的物料接觸,進行預還原 ;最後,將預還原後的氣體用於加熱和乾燥從反應器頂部加入的鐵精礦。 流態化焙燒 磁化焙燒 工藝,將貧鐵礦中的Fe2O3還原至有磁性的Fe3O4,然後用磁選法與脈石分離。用於反應的氫很少,但加熱貧鐵礦的熱量卻很大。所以,這一工藝將還原後的廢氣用空氣燃燒,在稀相流態化狀態下使加入的貧鐵礦預熱至略高於反應溫度;然後進入還原段,與煤氣中的氫和一氧化碳反應,生成Fe3O4。 流態化焙燒 流態化焙燒 流態化床 中與油或粉煤燃燒同時進行。所謂的快速流態化 床指的是圖1中u»uf的沸騰狀態,此時氣體和固體的接觸和混合都比經典的鼓泡型沸騰床更為優越,但是,為了保證床中有足夠量的固體料,必須將快速床頂部被氣體攜帶出的顆粒物料經鏇風器捕集後返回床底。 流態化焙燒 傾析 工藝在單一塔型設備內進行,且可採用極低的液固比 ,從而可自貧料 獲得較濃的溢流溶液。 流態化焙燒 流動規律 散式流態化流動規律 具有最簡單流動規律的流態化體系是以液體-固體為代表的散式流態化。如圖8左下方所示,在低流速時,床層為固定床,其壓降在對數坐標上隨液體的流速線性上升,而其空隙度維持一常數ε0。所謂空隙度 ε為床層中未被顆粒所占的空間體積與床層總體積之比。在流速u達到某一臨界值uf時,顆粒開始流態化,被液體所懸浮。從開始到全部流態化的流速區間一般很短。在達到流態化以後,所有顆粒被流體所懸浮,因此,從力的平衡考慮,流體通過顆粒料層的壓降與物料在液體中的有效重量相等,於是,壓降不再隨流速增加而增大,維持恆值。但是,顆粒床層卻隨著流速而上漲,空隙度加大。床層的上漲說明,隨著流速的加大,顆粒自動拉開其間距,容許更多流體流通而不增加阻力。對液-固體系而言,在對數坐標上,空隙度也隨著流速而近似線性上升,直至線速達到顆粒的自由沉降 速度ut時,ε=1,也即是說,此時,單個顆粒被懸浮於無窮大的液體中。 流態化焙燒 流態化系統 ,就可採用液、固相對速度代替上式中的流速u,從而形成廣義流態化 的關係式:
其中ud為固體的速度。從這一關係,可以定量地描述流體向上或向下、顆粒向上或向下、稀相或濃相、受阻沉降或移動床輸送等多種流態化操作,甚至包括加速運動。 隨機行走 產生離散的現象,完全不同。 流態化焙燒 兩相模型 。圖10表示了包括了暈的三相模型,即泡相、暈相和乳相。進入流態化床的氣流分為三部分,分別以uB、uC和uE的速度流入泡相B、暈相C和乳相E。泡相中顆粒甚少,氣-固反應一般可以忽略。在暈相和乳相中氣體按不同流型和固體反應。因此,在相鄰地區這三相中的氣體成分也不相同。泡相和暈相之間的氣體進行交換,在一定程度上使氣體成分趨於接近。同時,暈相和乳相之間的氣體以及固體顆粒也相互交換。按這一物理模型,即可寫出一組描述鼓泡床中氣-固行為的公式,為設計這種反應器提供方法。 流態化焙燒 流態化焙燒 焙燒反應器的設計和研製 流態化焙燒反應器的設計,與其他異相反應 裝置一樣,必須依靠對顆粒與氣體之間反應機理和速率、顆粒內部以及顆粒與氣體之間熱量和質量的傳遞、以及顆粒和流體的流型的了解。簡單的設計包括對反應器及其尺寸的選擇以及操作制度的確定。較高級的設計則包括對某種特定礦物及其加工工藝,從化學和工程原理出發研製合理的焙燒反應器。 無量綱數 Da: 流態化焙燒
其中k 為不包括擴散的本徵反應速率係數;De為擴散係數;R為顆粒的半徑。一般來說,若Da>25,需考慮由於擴散而帶來的阻力。 松粒 ,如圖12b所示。這樣,在堅粒的氣膜和產品層之外,還需加上堅粒之間的擴散。可以構想,接近團粒外圍的堅粒由於粒間擴散離氣體主流近,要比位於內部的堅粒反應得更快,如圖12b所示。 流態化焙燒 流態化焙燒 均勻球 體和流體的運動》,科學出版社,北京,1963。 郭慕孫:《流態化浸取 和洗滌》,科學出版社,北京,1979。 plenum ,New York,1980.配圖 相關連線
 流態化焙燒
流態化焙燒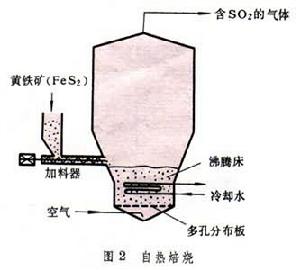 流態化焙燒
流態化焙燒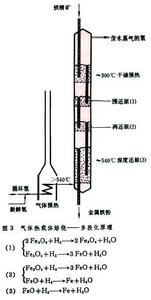 流態化焙燒
流態化焙燒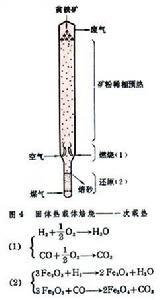 流態化焙燒
流態化焙燒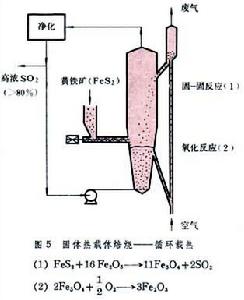 流態化焙燒
流態化焙燒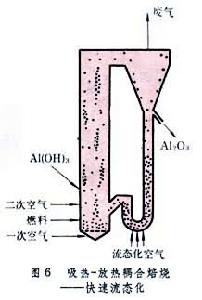 流態化焙燒
流態化焙燒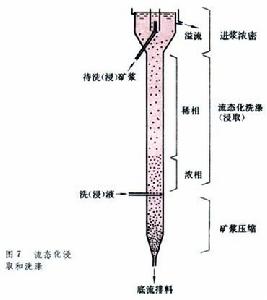 流態化焙燒
流態化焙燒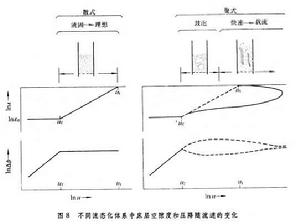 流態化焙燒
流態化焙燒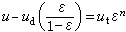
 流態化焙燒
流態化焙燒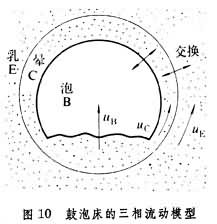 流態化焙燒
流態化焙燒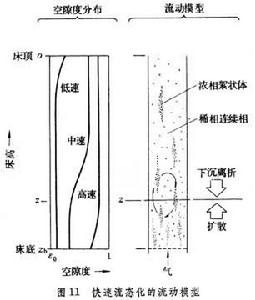 流態化焙燒
流態化焙燒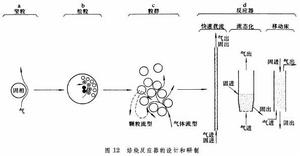 流態化焙燒
流態化焙燒
 流態化焙燒
流態化焙燒 流態化焙燒
流態化焙燒