介紹
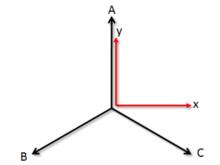 圖2
圖2從數學意義上講,park變換沒有什麼,只是一個坐標變換而已,從abc坐標變換到dq0坐標,ua,ub,uc,ia,ib,ic,磁鏈a,磁鏈b,磁鏈c這些量都變換到dq0坐標中,如果有需要可以逆變換回來。
從物理意義上講,park變換就是將ia,ib,ic電流在α、β軸上的投影,等效到d,q軸上,將定子上的電流都等效到直軸和交軸上去。對於穩態來說,這么一等效之後,iq,id正好就是一個常數了。
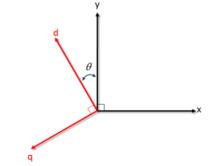 圖1
圖1從觀察者的角度來說,我們的觀察點已經從定子轉移到轉子上去,我們不再關心定子三個繞組所產生的旋轉磁場,而是關心這個等效之後的直軸和交軸所產生的旋轉磁場了。這樣做使得在建立轉子迴路電磁關係的微分方程時,其係數矩陣成為常數矩陣,而不是隨著時間和空間量變化的係數矩陣,這樣大大化簡了分析發電機、電動機的電磁關係的微分方程。
勻速圓周轉動的情況下,派克變換就是通過一定的角度旋轉變換,把旋轉中的向量變為靜止直角坐標系裡面的量,即將空間靜止坐標系代替旋轉坐標系。
定義
派克正變換:
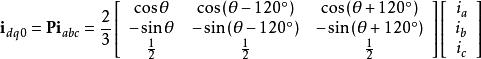 派克變換
派克變換逆變換:
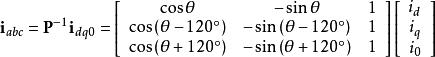 派克變換
派克變換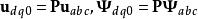 派克變換
派克變換派克變換也作用在定子電壓與定子繞組磁鏈上:
用派克變換化簡同步發電機基本方程
變換後的磁鏈方程
磁鏈方程:
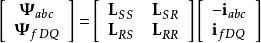 派克變換
派克變換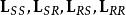 派克變換
派克變換上式中的電感係數矩陣 事實上都含有隨時間變化的角度參數,使得方程求解困難。
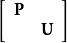 派克變換
派克變換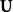 派克變換
派克變換現對等式兩邊同時左乘,其中為三階單位矩陣。方程化為:
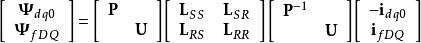 派克變換
派克變換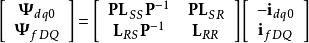 派克變換
派克變換 派克變換
派克變換其中
。① 變換後的電感係數都變為常數,可以假想dd繞組,qq繞組是固定在轉子上的,相對轉子靜止。
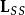 派克變換
派克變換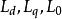 派克變換
派克變換② 派克變換陣對定子自感矩陣 起到了對角化的作用,並消去了其中的角度變數。為其特徵根。
③ 變換後定子和轉子間的互感係數不對稱,這是由於派克變換的矩陣不是正交矩陣。
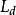 派克變換
派克變換④為直軸同步電感係數,其值相當於當勵磁繞組開路,定子合成磁勢產生單純直軸磁場時,任意一相定子繞組的自感係數 。
變換後的電壓方程
電壓方程:
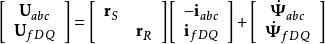 派克變換
派克變換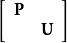 派克變換
派克變換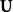 派克變換
派克變換現對等式兩邊同時左乘,其中為三階單位矩陣。方程化為:
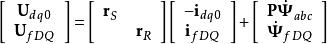 派克變換
派克變換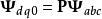 派克變換
派克變換由 ,
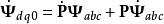 派克變換
派克變換對兩邊求導,得 ,
 派克變換
派克變換所以
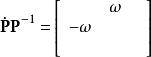 派克變換
派克變換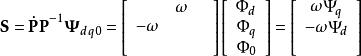 派克變換
派克變換其中 ,令
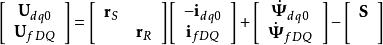 派克變換
派克變換於是有
上式右邊第一項為繞組電阻的壓降,第二項為變壓器電勢,第三項為發電機電勢或旋轉電勢。

