特性
在二維均勻流中，水流由於受到來自底部紊動渦體的作用，時均流速沿水深的分布是不均勻的，水面附近流速較大，河底附近流速較小，由河底向水面分成直線層、過渡層、對數區和外層區 。
直線層
也稱黏性底層，該層內流動為層流，只有黏滯切應力，流速分布成直線變化，計算公式為(1)
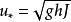河道水流流速分布
河道水流流速分布式中，u為距河底y處的點流速；，為摩阻流速；h為水深；J為能坡；g為重力加速度。直線層範圍是。
過渡層
該層流動由層流向紊流過渡，黏滯切應力與紊動切應力同時存在，流速分布由直線變化向對數曲線變化規律過渡，無統一計算公式，近似按直線層或對數區公式計算 。
對數區
河道水流流速分布該區的流動是紊流，以紊動切應力為主，流速分布呈對數曲線規律，一般公式形式為 (2)
河道水流流速分布式中，A和B是係數，與床面粗糙情況有關，通過實際資料確定，如愛因斯坦(H.A.Einstein)根據坎利根(G.H.Kenlegan)的分析提出的計算公式為
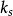河道水流流速分布
河道水流流速分布
河道水流流速分布式中，
為床面粗糙高度，可取床沙代表粒徑；x為反映對流速分布實際影響的係數，與值有關，為近壁層流層的厚度。直線層、過渡層和對數區合稱為內層區，區內流速分布主要受床面的影響 。
外層區
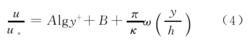河道水流流速分布該區內流動仍屬紊流，但流速分布除受床面的影響外，還要受到上游來流條件和上部邊界條件的影響，因而其分布規律偏離對數曲線而有一流速增值，公式的一般形式為
河道水流流速分布 河道水流流速分布式中，為尾跡強度係數；k為卡門常數；ω為函式符號，尚無理論解，只有一些近似假設；和k通過實測資料確定 。
實際套用
在實際工作中，通常將對數區的流速分布公式推廣到全部水深，根據全部水深上的流速分布資料來確定對數流速分布公式中的係數，再將對數流速分布公式用到全部水深上去。這樣做有一定近似，但從實用觀點看已基本滿足要求。
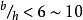河道水流流速分布在寬深比不大（，b為河寬，h為水深）的河槽中，斷面上任一點的水流不僅受到來自河底紊動渦體的作用，還同時受到來自河岸紊動渦體的作用。縱向流速不僅沿水深變化，沿斷面橫向分布也是不均勻的，接近河岸的垂線與河心的垂線流速分布相差較大，岸邊垂線的最大流速往往不在水面上。河槽過於窄深時，河中心垂線的最大流速也不在水面。
在挾沙水流中，泥沙顆粒的存在對水流紊動結構有一定影響，因而其流速分布與清水水流也有所不同 。
