基本介紹
 氣相湍流
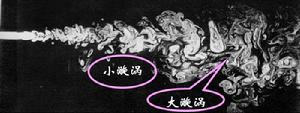
氣相湍流氣相湍流是氣相流體的一種流動狀態。當流速很小時,流體分層流動,互不混合,稱為層流,也稱為穩流或片流;逐漸增加流速,流體的流線開始出現波浪狀的擺動,擺動的頻率及振幅隨流速的增加而增加,此種流況稱為過渡流;當流速增加到很大時,流線不再清楚可辨,流場中有許多小漩渦,層流被破壞,相鄰流層間不但有滑動,還有混合,形成湍流,又稱為亂流、擾流或紊流。
在自然界中,我們常遇到流體作湍流,如江河急流、空氣流動、煙囪排煙等都是湍流。
氣相湍流是在大雷諾數下發生的,雷諾數較小時,黏滯力對流場的影響大於慣性力,流場中流速的擾動會因黏滯力而衰減,流體流動穩定,為層流;反之,若雷諾數較大時,慣性力對流場的影響大於黏滯力,流體流動較不穩定,流速的微小變化容易發展、增強,形成紊亂、不規則的湍流流場。
 氣相湍流
氣相湍流流態轉變時的雷諾數值稱為臨界雷諾數。一般管道雷諾數Re=4000為湍流狀態,Re=2320~4000為過渡狀態。
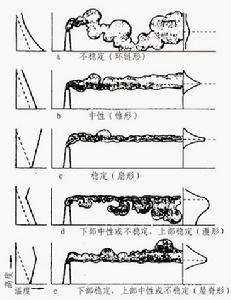
氣相湍流基本特徵是流體微團運動的隨機性。湍流微團不僅有橫向脈動,而且有相對於流體總運動的反向運動,因而流體微團的軌跡極其紊亂,隨時間變化很快(見右圖)。湍流中最重要的現象是由這種隨機運動引起的動量、熱量和質量的傳遞,其傳遞速率比層流高好幾個數量級。
湍流利弊兼有。一方面它強化傳遞和反應過程;另一方面極大地增加摩擦阻力和能量損耗。鑒於湍流是自然界和各種技術過程中普遍存在的流體運動狀態(例如,風和河中水流,飛行器和船舶表面附近的繞流,流體機械中流體的運動,燃燒室、反應器和換熱器中工質的運動,污染物在大氣和水體中的擴散等),研究、預測和控制湍流是認識自然現象,發展現代技術的重要課題之一。氣相湍流研究主要有兩類基本問題:闡明湍流是如何發生的;了解湍流特性。由於湍流運動的隨機性,研究湍流必需採用統計力學或統計平均方法。研究湍流的手段有理論分析、數值計算和實驗。後二者具有里要的工程實用意義。
湍流理論
中心問題是求湍流基本方程納維-斯托克斯方程的統計解,由於此方程的非線性和湍流解的不規則性,湍流理論成為流體力學中最困難而又引人入勝的領域。雖然湍流已經研究了一百多年,但是迄今還沒有成熟的精確理論,許多基本技術問題得不到理論解釋。
1895年,O.雪諾首先採用將湍流瞬時速度、瞬時壓力加以平均化的平均方法,從納維-斯托克斯方程導出湍流平均流場的基本方程——雷諾方程,奠定了湍流的理論基礎。以後發展了(以混合長假設為中心的)半經驗理論和各種湍流模式,為解決各種迫切的技術問題提供了一定有效的理論依據。20世紀30年代以來,湍流統計理論,特別是理想的均勻各向同性湍流理論獲得了長足的進步,但是離解決實際問題還很遠。60年代以來套用數學家採用泛函、拓撲和群論等數學工具,分別從統計力學和量子場論等不同角度,探索湍流理論的新途徑。70年代以來,由於湍流相干結構(又稱擬序結構)概念的確立,專家們試圖建立確定性湍流理論。關於湍流是如何由層流演變而來的非線性理論,例如分岔理論,混沌理論和奇怪吸引子等有了重要進展。
分類
微觀模擬
目前,基於連續介質理論體系下的湍流微觀模型包括直接求解N—S方程(DNS)、大渦模擬(LES)、離散渦模擬(DVS)三類。
DNS方法是在湍流尺度下的格線尺寸內不引入任何封閉模型的前提下對N—S方程直接求解。這種方法能對湍流流動中最小尺度渦進行求解,其所得結果的誤差僅是一般數值計算所引起的那些誤差,並且可以據需要而加以控制,但必須採用很小的時間與空間步長以達到統計的穩定狀態,因此,DNS方法僅限於很小空間內相對低的雷諾數和簡單邊界條件的湍流流動模擬,如槽道流動與平板邊界層流動;另外由於DNS方法計算量很大,目前尚無法用於工程問題。
LES方法的基本思想是:湍流流動是有許多大小不同尺度的渦旋組成,大尺度的渦旋對平均流動影響比較大,各種變數的湍流擴散、熱量、質量、動量和能量的交換以及雷諾應力的產生都是通過大尺度渦旋來實現的,而小尺度渦旋主要對耗散起作用,通過耗散脈動來影響各種變數。由於格線尺度比湍流尺度大,可以模擬湍流發展過程中的一些細節,用於比較簡單的剪下流運動和管流。由於LES方法計算精度可與DNS方法相比,LES方法可得到真實瞬態流場精度相當高,但其計算費用卻便宜得多,所以近幾十年來得到飛快發展。目前該模型主要用於檢驗統觀模型。
離散渦或隨機渦模擬是把湍流流場分成一系列大尺度渦元,用渦元的隨機運動來模擬湍流。它能獲得混合層和尾渦中大尺度渦旋機理的本質,目前也得到了一定程度的套用[54]。總的來說,離散渦模擬(DVS)仍是比較新的求解N—S方程的一種數值方法,尚處於形成階段。最主要的原因是定性上描述尚可而定量上精度難以確定。就已得到的結果而言,只能給出合理的現象。其主要問題是:(1)渦旋尺寸分布的確定有任意性;(2)未考慮含能渦和耗散渦的差別;(3)尚難以用於三維問題。
機率密度函式模擬
近年來,由分子運動理論推導的機率密度函式(Probability Density Funtion)輸運方程,簡稱PDF模型。與通常的湍流模型相比,PDF模型能夠對湍流流場進行更為精確和完整的描述。套用PDF模型計算的平面混合層流流動、平面尾流、平面射流和軸對稱射流四種剪下流動的擴展率、平均速度的分布和Reynolds應力的計算值與試驗值吻合較好。用這種方法對湍流自由射流進行模擬,得到的射流擴張率、平均速度及Reynolds應力與試驗值十分吻合。採用PDF模型模擬湍流燃燒和污染物的生成的較多。
統觀模擬
在單相湍流領域內,上述兩種模擬方法在工程套用上的困難,按國內外一些學者的看法,可用於工程套用上的現實模擬方法是雷諾方程組與關聯矩封閉方法。它將雷諾時均方程及湍流特徵量輸運方程中的高階未知關聯項用低階未知關聯項或時均量來表達,從而使雷諾時均方程封閉。對於這些關聯量的處理,有各種模型:湍流粘性係數模型、代數雷諾應力模型(ASM)、雷諾應力模型(DSM)。而其中較為常見、較為有效的是k-ε雙方程模型和雷諾應力模型。k-ε雙方程模型相對來說較為簡單,使用方便,適合工程問題的研究,目前套用得最多,對其解決各種流動問題的有效性也認識得最清楚。
k-ε雙方程模型有以下優點:(1)通過求偏微分方程考慮湍流物理量的輸運過程,即通過求解偏微分方程確定脈動特徵速度與平均場速度梯度的關係,而不是直接將兩者聯繫起來;(2)特徵長度不是由經驗確定,而是以耗散尺度作為特徵長度,並由求解相應的偏微分方程得到。
k-ε雙方程模型在套用時也有其局限性:它不能用於低雷諾數的層流條件,適合用於高雷諾數、充分發展的湍流流動區域。基於各向同性的標準k-ε雙方程模型可以較成功的模擬無浮力平面射流、平壁邊界層、管流及有弱旋的回流流動;而對強旋流、浮力流、重力分層流以及曲壁邊界層和低雷諾數流動問題,有很大的缺陷。這主要有兩方面的原因:一方面是因為k-ε模型中ε方程模擬的不準確性,另一方面是因為採用了各向同性渦粘係數的Boussinesq假設,無法預報各向異性很強的湍流流動。一般認為Sn(旋流數)﹤0.5以下,採用各向同性的湍流粘性係數模型,這時標準的k-ε雙方程模型能較好地預報流場內的分布特性,當Sn﹥1時,標準的k-ε雙方程模型的預報是不成功的,必須對標準的k-ε雙方程模型進行修正。

