定義
在量子力學裡,表達粒子的量子態的波函式必須滿足 歸一條件( 歸一化,英語:be normalized),也就是說,在空間內,找到粒子的機率必須等於1。這性質稱為 歸一性。用數學公式表達,
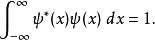 歸一條件
歸一條件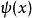 歸一條件
歸一條件其中,x是粒子的位置,是波函式。
歸一化導引
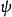 歸一條件
歸一條件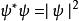 歸一條件
歸一條件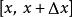 歸一條件
歸一條件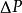 歸一條件
歸一條件一般而言,波函式是一個複函數。可是,是一個實函式,大於或等於0,稱為“機率密度函式”。所以,在區域內,找到粒子的機率 是
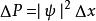 歸一條件
歸一條件;(1)。
既然粒子存在於空間,機率是1。所以,積分於整個一維空間:
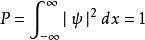 歸一條件
歸一條件。(2)
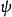 歸一條件
歸一條件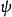 歸一條件
歸一條件假若,從解析薛丁格方程而得到的波函式,其機率P是有限的,但不等於1,則可以將波函式乘以一個常數,使機率P等於1。或者,假若波函式內,已經有一個任意常數,可以設定這任意常數的值,使機率P等於1。
歸一化恆定性
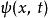 歸一條件
歸一條件給予一個歸一化的波函式。隨著時間的變化,波函式也會改變。假若,隨著時間改變的波函式不再滿足歸一條件,則勢必要重新將波函式歸一化。這樣,歸一常數A變得含時間。很幸運地,滿足薛丁格方程的波函式的歸一性是恆定的.設定波函式滿足薛丁格方程與歸一條件:
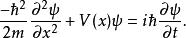 歸一條件
歸一條件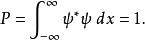 歸一條件
歸一條件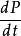 歸一條件
歸一條件假若,歸一性是恆定的,則機率P不含時間。為了顯示這一點,先計算 :
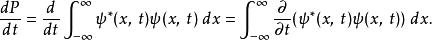 歸一條件
歸一條件展開被積函式
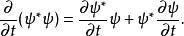 歸一條件
歸一條件編排薛丁格方程,可以得到波函式對於時間的偏導數:
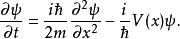 歸一條件
歸一條件共軛波函式對於時間的偏導數為
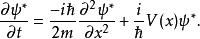 歸一條件
歸一條件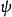 歸一條件
歸一條件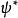 歸一條件
歸一條件將與代入被積函式
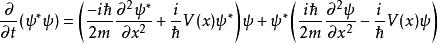 歸一條件
歸一條件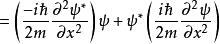 歸一條件
歸一條件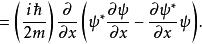 歸一條件
歸一條件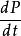 歸一條件
歸一條件代入的方程:
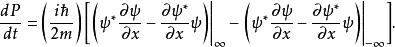 歸一條件
歸一條件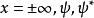 歸一條件
歸一條件可是,在都等於 0 .所以,
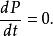 歸一條件
歸一條件機率 P=1 不含時間。波函式的歸一化是恆定的。
實例
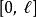 歸一條件
歸一條件在一維空間內,束縛於區域內的一個粒子,其波函式是
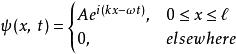 歸一條件
歸一條件;
 歸一條件
歸一條件其中,k是波數,是角頻率,A是任意常數。
計算能夠使波函式歸一化的常數值A。將波函式代入:
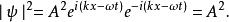 歸一條件
歸一條件積分於整個粒子存在的區域:
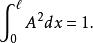 歸一條件
歸一條件稍加運算,
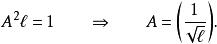 歸一條件
歸一條件歸一化的波函式是:
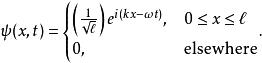 歸一條件
歸一條件
