基本介紹
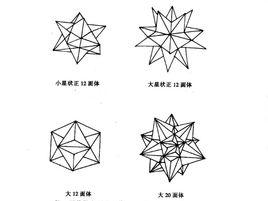
正多面體中除了五種凸正多面體(又稱“柏拉圖立體”)外,還有四種 正星體,它們是凹正多面體,克卜勒(Kepler)與普安索(Poinsot)發現了這4種內凹的正多面體,故又把這四種正星體稱為Kepler-Poinsot多面體。四種正星體分別是如圖1至圖4所示的正六角星體、正八角星體(各有24個面)和正十二角星體、正二十角星體(各有60個面)。
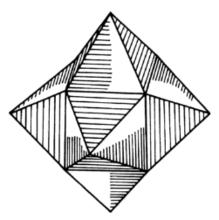 圖1 正六角星體 圖1 正六角星體 | 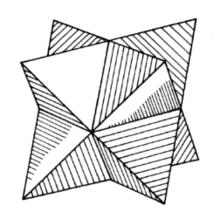 圖2正八角星體 圖2正八角星體 |
 圖3 正十二角星體 圖3 正十二角星體 | 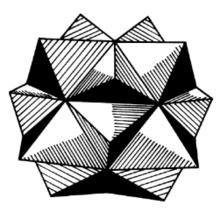 圖4正二十角星體 圖4正二十角星體 |
克卜勒與普安索的發現
克卜勒研究過正多面體(每個面皆為全等的正多邊形的幾何體),他知道:早在古希臘時期,哲人柏拉圖已發現了五種正多面體(正4、6、8、12、20面體,後來人們發現:凸正多面體僅有上面五種),對於非凸的情形又將如何?
首先,克卜勒(Kepler)發現了兩種各面均為全等三角形的凹正多面體:小星狀正十二面體和大星狀正十二面體。1809年波因素特(Poinsot)(即普安索)又發現了兩種凹正多面體(每面皆為全等三角形):大十二面體和大二十面體。
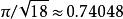 正星體
正星體附記 克卜勒在研究天體運動時,還涉及了一些數學特別是幾何問題。1611年他曾斷言:在一個大立方體中堆放半徑一樣的小球,小球總體積與立方體積之比ρ不超過(克卜勒猜想)。這是一個至今尚未解決(證明)的結論,儘管人們對它的正確性並不懷疑,儘管人們對比值ρ不斷改進,到目前為止,人們證明的最好結果是ρ≤0.7731,這是由數學家穆德(D.J.Muder)於1993年給出的 。
四種正星體的介紹
小星狀正十二面體
正二十面體同一面的五個相鄰面延展後,交於一點,與底面形成正五稜錐(圖5)。類似的作法,其他十一個面上都會形成全等的正五稜錐。這種含十二個正五稜錐的星體稱為小星狀正十二面體(Small Stellated Dodecahedron),它的直觀圖如圖版6左,平面圖如圖版6右。其面數,頂點數,棱數分別為f=12,v=12,e=30。
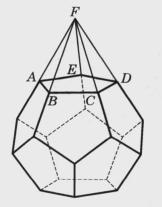 圖5
圖5這一星體作法的等價說法是:延展正十二面體各面所在平面(圖版6左),十二平面兩兩相交,形成十二個五角星形,正十二面體同一面上也同樣出現十二個正五稜錐 。
 圖6
圖6 小星狀正十二面體的平面展開圖
小星狀正十二面體的平面展開圖大正十二面星體
星體構造法減法中從正二十面體十二個對頂面使兩兩相交,相交面的公共部分出現一個凹多面體,這個立體就是第二種克卜勒一普安索體。不妨構想在圖7中正二十面體的D點有五條棱通過:DA、DE、DI、DH、DC。AEIHC為一平面正五邊形,是正二十面體一個對頂面。除了對頂面LGBFJ與它平行外,其餘十個對頂面與它兩兩相交,形成了一朵美麗的立體五角星(圖8)。十二個對頂面上都出現了同樣的立體,它們的全體就構成了 大正十二面星體(Great Dodecahedron)。其面數,棱數,頂點數分別為12,30,12。其面數,頂點數,棱數分別為f=12,v=12,e=30。
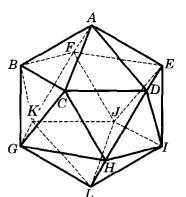 圖7
圖7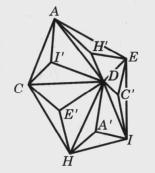 圖8
圖8之所以稱為十二面是因為它的十二個角頂分別對應一個正五角星形對頂面,它的直觀圖如圖版9左,平面圖為圖版9右,它是小星狀十二面體的對偶圖形 。
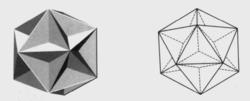 圖9
圖9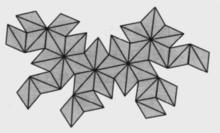 大正十二面星體的平面展開圖
大正十二面星體的平面展開圖大星狀正十二面體
大星狀正十二面體是從大正十二面星體經過加法構造出來的。就在大正十二面星體外添加了二十個正三稜錐,它們的全體就是大星狀正十二面星體(Great Stellated Dodecahedron)。之所以稱為大星狀正十二面星體是因為它有十二個面。其面數,頂點數,棱數分別為f=12,v=20,e=32。
大星狀正十二面體作法的等價說法是:從大正十二面星體做加法,延展它的十二個面,使兩兩相交,在形外產生二十個正五稜錐,在同一延展面上的五邊形擴展成正五角星,從此也就輕便地獲知大星狀正十二面體上每一正五稜錐的側面也是以底角72 、頂角36 形成的等腰三角形。
另一方面,我們還有興趣地看到,大星狀正十二面體的核心恰是一個以它的正三稜錐底棱作為棱的正二十面體。因此它的模型是很容易製作的。
大正二十面星體
大正二十面星體是從正二十面體的二十個面延展構成的。構造構想十分奇巧。其面數,頂點數,棱數分別為f=20,v=12,e=30 。