簡介
不需要外加激勵信號,電路就能產生輸出信號的電路稱為信號發生電路或波形振盪器.其中能產生正弦波輸出信號的電路稱為正弦波發生電路或正弦振盪器
電路圖
.文氏橋振盪器
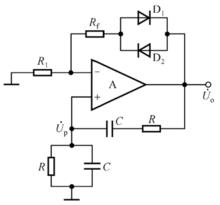文氏橋振盪器產生條件
1. 正弦波振盪電路
為了產生正弦波，必須在放大電路里加入正反饋，因此放大電路和正反饋網路是振盪電路的最主要部分。但是，這樣兩部分構成的振盪器一般得不到正弦波，這是由於很難控制正反饋的量。
如果正反饋量大，則增幅，輸出幅度越來越大，最後由三極體的非線性限幅，這必然產生非線性失真。反之，如果正反饋量不足，則減幅，可能停振，為此振盪電路要有一個穩幅電路。
為了獲得單一頻率的正弦波輸出，應該有選頻網路，選頻網路往往和正反饋網路或放大電路合而為一。選頻網路由R、C和L、C等電抗性元件組成。正弦波振盪器的名稱一般由選頻網路來命名。
因此,正弦波振盪電路由放大電路、正反饋網路、選頻網路、穩幅電路組成。
2. 振蕩平衡條件
產生正弦波的條件與負反饋放大電路產生自激的條件十分類似。只不過負反饋放大電路中是由於信號頻率達到了通頻帶的兩端，產生了足夠的附加相移，從而使負反饋變成了正反饋。在振盪電路中加的就是正反饋，振盪建立後只是一種頻率的信號，無所謂附加相移。
圖1 負反饋放大電路和正反饋振盪電路框圖比較
正反饋一般表達式：
振盪條件為：
包括振幅平衡條件：，
相位平衡條件：JAF= jA+jF=±2np
3. 起振條件和穩幅原理
振盪器在剛剛起振時，為了克服電路中的損耗，需要正反饋強一些，即要求。
既然，起振後就要產生增幅振盪，需要靠三極體大信號運用時的非線性特性去限制幅度的增加，這樣電路必然產生失真。這就要靠選頻網路的作用，選出失真波形的基波分量作為輸出信號，以獲得正弦波輸出。
也可以在反饋網路中加入非線性穩幅環節，用以調節放大電路的增益，從而達到穩幅的目的。
自激振盪原理
信號發生電路能產生各種波形的輸出信號,都是基於自激振盪原理.自激振盪原理的方框圖如圖1所示:
基本放大器
A
反饋網路
F
+
它是由基本放大器A和正反饋網路F組成的閉合正反饋環路.
圖1(X為電量:電壓或電流)
A和F分別為基本放大器和反饋網路的正向傳輸函式,即:
+
圖1中的 為相加器,
因此圖1的輸出:
(1)
(2)
(3)
由於自激振盪是一種沒有輸入( ),仍有一定大小輸出( 非零值)的電路,因此,由式(3)必須有:
或
(4)
即:
1,自激振盪器是由放大器A和反饋網路F組成的閉合環路,其 能形成自激振盪須滿足:
稱 為自激振盪條件.
由於A,F為複數形式,故自激振盪條件又可以表示為:
及 n=0,1,2… Z為整數
上式中第一項為自激振盪的幅度條件,第二項為自激振盪的相位條件.
相位條件是產生自激振盪的必要條件,即反饋信號 必須與放大器A的輸入信號 同相(正反饋),幅度條件則是自激產生的充分條件,兩者缺一不可.
2,環路增益函式T
由A 和 F組成的閉合環路,若在環路中的某一處斷開,分別作為環路的輸入和輸出,它們的比值就是環路增益函式,即:
圖2
由於是閉合環路,原則上在哪處斷開都可以.
對於圖1所示的方框圖,由於 ,
若取相加處為環路的起始和終點,則有:
(6)
所以自激振盪條件又可用環路增益函式表示:
或
(7)
式(6)(7)說明:當反饋網路的輸出 從相位和幅度大小上完全等同於放大器輸入 時,自激振盪形成,電路有輸出 .
3,正弦波發生電路的輸出是單一頻率的正弦波,因此由圖1電路實現正弦振盪的條件是滿足式(5)或式(7)的頻率應該是唯一的所以閉合環路中的反饋網路F通常為具有選頻特性的.選頻特性的Q值越高,則電路產生的正弦波越純,越好.
利用式(5)或式(7),我們可以分析求解出正弦波發生電路的振盪頻率和起振條件.
二,自激振盪的建立和形成
1,由閉合環路組成的自激振盪器,其振蕩產生的起始信號來自於電路中的各種起伏和外來擾動,例如電路接通電源瞬間的電衝擊,電子器件的噪聲電壓等等,這些電信號中含豐富的頻率成分,經選頻網路
選出某頻率的信號輸送至放大器A放大後,經F網路反饋後再放大,……,反覆循環直至電路的輸出Xo由小至大.最後建立和形成穩定的波形輸出.
2,為使振盪器的輸出穩定在一定的幅度,放大器A必須為具有非線形傳輸特性的,如圖3(a)所示.一般,反饋網路的傳輸特性為線形的,如圖3(b).
圖3(a)
圖3(b)
由於自激振盪器是閉合環路,F網路的輸入Xo就是A放大器的輸出,F網路的輸出Xd就是A的輸入,因此,可以將圖3(a)和(b)合併畫在同一個圖上,如圖(4),這樣便於分析閉合環路中放大,反饋,放大……的反覆循環過程.
圖(4)
由圖4可以看到,放大器輸入Xd1,經A放大得Xo1,Xo1經F網路得到Xf1 =Xd2,Xd2經F網路得到Xf2 =Xd3……,最後到達|A|和1/|F|的交點_B,振盪形成.稱B點為振盪形成的平衡點,B點對應的輸出XoB為振盪形成的輸出大小.
上述分析表明:
①,對圖4中,B點以下的部分有
即|AF|>1,這時電路中的任何擾動都會經過閉合環路的多次循環放大,變得越來越大.
②在B點有 ,即|AF|=1,滿足自激振盪的幅度條件.
③B點以上的部分,有 ,即|AF|0 為電感
若X0,以及電阻
因此式(9)中須有 .即X1和X3必須是同類電抗.
而為滿足(8)式,可知X2必須為和X1,X3的相反類電抗.例如X1,X3為電感時X2必須為電容.
②通常分析時,由式(8)解得三點式振盪器的振盪頻率,由式(9)求得電路的起振條件.
4,電容三點式振盪器
X1和X3取電容,X2取電容,如圖9所示.
圖9
由式(8)得
振盪頻率
由式(9)得電路的起振條件
5,電感三點式振盪器
X1和X3取電容,X2取電感,如圖10所示.
圖10
振盪頻率
由式(9)得電路的起振條件
6,由雙極型電晶體(BJT)構成的三點式振盪器分析
圖11(a)
圖11(a)為交流電路,圖11(b)為電晶體用低頻等效電路替代的交流等效電路,其中設
採用圖11(b)進行分析的時,若能忽略hie的分流作用,即
則圖11(b)電路分析與圖8電路完全相同,其結論完全適用圖11.所以通常由BJT構成的三點式振盪器時,大多要求滿足
圖11(b)
五,石英晶體振盪器
1,石英晶體諧振器的阻抗特性
利用石英晶體的壓電效應製作的具有高Q值諧振特性的器件,其符號及等效電路如圖12(a)所示,其中
圖12(a)
圖12(b)
C0——靜態等效電容,幾pF～幾十pF
C1——彈性慣性的等效電容
10-2～10-4pF
L——機械振動慣性等效電感
幾十mH～幾百H
R——振動時摩擦等效電阻,其值很小,幾十歐姆以下,常可忽略.
從圖12(b)可求出石英晶體的連線埠等效阻抗:
即:
通常定義兩種諧振頻率:
①串聯諧振頻率
②並聯諧振頻率
由於C0>>C1,可以有 :
即ωp略大於ωs,但兩者十分接近.
將ωp,ωs代入Z(jω)式中:
式(10)
由式(10)畫得X(ω)～ω曲線:
從圖13有:
①當ωωp時,X(ω)
套用
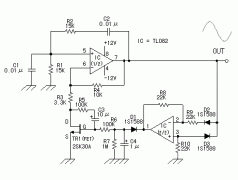
數字正弦波發生器電路圖
如圖所示為數字正弦波發生器。它由模擬數字轉換器(4018B)和一個固定濾波器(MAX29X)構成。時鐘脈衝輸入CP的一部分驅動MAX29X濾波器，另一部分被第一個10位計數器(4018B)分頻，再由第二個l0位計數器分頻，輸出的階梯波經R5和Cl的作用使其轉變為平滑的正弦波，再經濾波器濾波後輸出。電路的輸出頻率隨時鐘輸入而變，其關係為fout=fin/l00。
