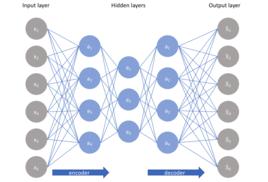
提出背景
編碼維數小於輸入維數的欠完備自編碼器可以學習數據分布最顯著的特徵。我們已經知道，如果賦予這類自編碼器過大的容量，它就不能學到任何有用的信息。
如果隱藏編碼的維數允許與輸入相等，或隱藏編碼維數大於輸入的過完備（overcomplete）情況下，會發生類似的問題。在這些情況下，即使是線性編碼器和線性解碼器也可以學會將輸入複製到輸出，而學不到任何有關數據分布的有用信息。
理想情況下，根據要建模的數據分布的複雜性，選擇合適的編碼維數和編碼器、解碼器容量，就可以成功訓練任意架構的自編碼器。正則自編碼器提供這樣的能力。
定義
正則自編碼器使用的損失函式可以鼓勵模型學習其他特性（除了將輸入複製到輸出），而不必限制使用淺層的編碼器和解碼器以及小的編碼維數來限制模型的容量。這些特性包括稀疏表示、表示的小導數、以及對噪聲或輸入缺失的魯棒性。即使模型容量大到足以學習一個無意義的恆等函式，非線性且過完備的正則自編碼器仍然能夠從數據中學到一些關於數據分布的有用信息。
原理
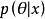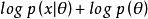正則自編碼器
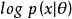正則自編碼器
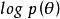正則自編碼器
正則自編碼器
正則自編碼器我們可以簡單地將懲罰項Ω(h) 視為加到前饋網路 的正則項，這個前饋網路的主要任務是將輸入複製到輸出（無監督學習的目標），並儘可能地根據這些稀疏特徵執行一些監督學習任務（根據監督學習的目標）。不像其它正則項如權重衰減——沒有直觀的貝葉斯解釋。權重衰減和其他正則懲罰可以被解釋為一個MAP 近似貝葉斯推斷，正則化的懲罰對應於模型參數的先驗機率分布。這種觀點認為，正則化的最大似然對應最大化，相當於最大化。即通常的數據似然項，參數的對數先驗項則包含了對特定值的偏好。正則自編碼器不適用這樣的解釋是因為正則項取決於數據，因此根據定義上（從文字的正式意義）來說，它不是一個先驗。雖然如此，我們仍可以認為這些正則項隱式地表達了對函式的偏好。
