簡介
正交增量過程(process with orthogonal increments)是一種隨機過程。指在不相交區間上的增量不相關的隨機過程。復值隨機過程{X(t)，t∈T}稱為正交增量過程，如果對所有t，s∈T有E|X(t)-X(s)|<+∞，且對t，t，t，t∈T，t<t≤t<t，有E{(X(t)-X(t)}=0。
定義
正交增量過程是在任何兩個不相交時段上增量有正交性的隨機過程。設{X，t∈T}為復值二階矩過程，如對任何參數t<t≤t<t，總有 (正交性)：
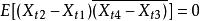正交增量過程則稱此過程為正交增量過程。“正交”名稱來源如下：以O記所有二階矩有限的復值隨機變數的全體，在O中引入內積：
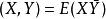正交增量過程當內積為0時，稱X與Y正交。這是歐氏空間中向量正交性的一種推廣。當{X，t∈T}為常值均值的正態過程時，正交增量性與獨立增量性一致。
隨機過程
隨機過程是一種數學結構。實際中的隨機過程是指由於隨機因素影響而受機率規律支配的過程。而數學上的隨機過程則是由實際隨機過程概念構成的一種數學結構。具體地，當客觀世界中某些被研究的系統(或更一般地說，對象)的狀態不僅具有偶然性，而且還隨時間(或位置)的變化而改變，例如，某海區不同地點的浪高，某人一天中體溫的變化等。這就是說，要考慮一些隨機現象的發展和變化過程，其中要涉及無窮多個有一定內部聯繫的隨機變數，人們就把這樣的一族隨機變數稱為隨機過程.在數學上，利用測度論可定義隨機過程如下：設給定參數集合T和可測空間(E，B).若對每一t∈T，有一個定義在機率空間(Ω，F，P)上的E值B可測函式(即隨機變數)X(t，ω) (ω∈Ω)，與之對應，則稱依賴於參數t的可測函式集合{X(t，ω)，t∈T}為定義在(Ω，F，P)上取值於(E，B)中的隨機過程(也可稱為隨機函式).當空間(Ω，F，P)和(E，B)已明確固定時，簡稱隨機過程並記為{X(t)，t∈T}.空間(E，B)稱為狀態空間或相空間，E中的元素稱為狀態.最常見的情形是狀態可用一個數來描述，這時狀態空間E是一數(實數或複數)集，對應的隨機過程稱為數值的。
一般地，參數集T不一定限於數集，它可以是向量集、集族或更一般的抽象元素集。但是在大多數情形中，參數集T是一個有限或無窮區間，或者是一整數集合，這時人們常常賦予參數t以時間的含義，而且把前一種情形稱為連續參數隨機過程，後一種情形稱為離散參數隨機過程或隨機序列。
由以上定義看出，對每一固定的t∈T，X(t，·)是定義在(Ω，F，P)上的一個隨機變數，對每一固定的ω∈Ω，X(·，ω)是定義在參數集T上的函式——過程的樣本函式。除了可以把隨機過程看做是一族隨機變數{X(t，·)，t∈T}外，還可以把它看做是乘積空間E(或者說樣本函式空間)上由映射ψ：ω↦X(·，ω)∈E誘導出E上的機率測度Pψ，或者把它看做是乘積空間T×Ω上滿足某種可測性的E值(二元)函式。第一種看法便於把隨機過程和隨機變數、隨機向量聯繫起來並看做是它們的自然推廣。第二種看法有明顯的理論長處.而第三種看法則便於對隨機過程的可測性(如二元可測、循序可測、可選和可料等)作細緻分類。一個隨機過程的機率分布律可由規定它的隨機變數的有限維聯合分布給出。根據其中的隨機變數之間聯繫的統計特性或其他特徵，可以對隨機過程進行分類。平穩過程、馬爾可夫過程、獨立增量過程、鞅、分支過程和隨機點過程就是當今研究得較多且用途較廣的幾大類。
獨立增量過程
獨立增量過程亦稱可加過程。一類重要的隨機過程。如果對任意0≤t<t<…<t，n≥1，X(t)，X(t)-X(t)，…，X(t)-X(t)相互獨立。則稱隨機過程{X(t)，t≥0}為獨立增量過程。獨立增量過程也是馬爾可夫過程。有些文獻只要求X(t)-X(t)，…，X(t)-X(t)相互獨立。一般地，這兩個定義是不完全一樣的。但是，如果加上對初始狀態的假設X(0)=1，則兩者相同。這時過程的有限維分布可由增量分布確定。獨立增量過程是一類很廣泛和重要的隨機過程。泊松過程和維納過程都是獨立增量過程。過程的獨立增量性質也稱“無後效性”或“無記憶性”。
平穩過程
統計特性不隨時間的推移而變化的隨機過程。平穩過程的基本理論是在20世紀30—40年代建立和發展起來的，並已相當完善。1934年原蘇聯數學家辛欽發表了《平穩過程的相關理論》一文，為平穩過程奠定了理論基礎。其後的研究主要是向某些特殊類型以及多維平穩過程、平穩廣義過程和齊次隨機場等方面發展。平穩過程理論在無線電技術和自動控制等領域有著廣泛的套用，並且是諸如時間序列分析、信號分析、濾波、預測理論以及控制理論等套用學科的重要工具。將傅立葉分析方法套用於寬平穩過程，可以把過程表成有不相關隨機振幅的簡諧振動的疊加，這就產生了過程按頻率的譜分解，它是寬平穩過程的一個基本結果，由此可以推出一些重要的結論，例如均方大數律。柯爾莫戈羅夫和N.維納在1940年左右提出並解決了一維寬平穩過程的線性預報問題，關於多維寬平穩過程的線性預測問題，也有類似一維的結果。平穩過程的線性預測理論，後來又被許多人所研究。這個理論是平穩過程論當中有重要地位的一個分支，它從通訊、電工學開始被套用於各個方面。齊次隨機場是一種平穩過程，它在力學的湍流理論中很有用，齊次場的線性預測問題比寬平穩過程的情形要複雜得多，中國學者江澤培在這方面的工作有一定成果。
