基本介紹
歐拉類
歐拉類歐拉類是實向量叢底空間的一個上同調類，定向實n維向量叢的歐拉類是上同調類，在標準同構
歐拉類
歐拉類
歐拉類
歐拉類
歐拉類
歐拉類下，它對應於，其中u是中惟一的上同調類，限制在中是標準的定向類。這裡的為全空間，為底空間。
歐拉類的性質
歐拉類的性質：
歐拉類
歐拉類
歐拉類1．自然性。若被一個保定向的叢映射覆蓋，則。
歐拉類
歐拉類2．若把的定向反向，則歐拉類變號。
歐拉類3．若纖維維數n是奇數，則
歐拉類 歐拉類
歐拉類4．自然同態把歐拉類變為施蒂費爾一惠特尼類。
歐拉類5．惠特尼和的歐拉類滿足。類似地，笛卡兒積的歐拉類滿足
歐拉類 歐拉類 歐拉類6．若定向向量叢具有一個處處為零的截面，則其歐拉類必為零。
相關概念
示性類
纖維叢通常用一些拓撲不變的整數(稱為示性數)來標誌其和平庸叢的偏離，當我們引人聯絡以後，這些示性數可以用由聯絡表示的示性類在整個底流形上的積分表示出來。但積分的結果(示性數)與聯絡的選擇無關，是拓撲不變數。在纖維叢上可以定義很多不同的示性類，如斯蒂弗爾-惠特尼類、龐特里亞金(Pontrjagin)類、陳(陳省身)類和歐拉類等。對於2n維黎曼流形，歐拉類定義為
歐拉類歐拉類對底流形積分即得歐拉數
歐拉類此即高斯-博內(Gauss-Bonnet)定理，是更一般的阿蒂亞-辛格(Atiyah-Singer)指標定理的特例 。
陳(省身)類
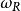歐拉類
歐拉類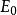
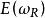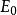歐拉類 歐拉類
歐拉類
歐拉類 歐拉類 歐拉類 歐拉類 歐拉類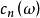
歐拉類
歐拉類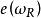
歐拉類
歐拉類陳(省身)類(Chern class)是復向量叢的一種上同調類。設ω為復n維向量叢，為其基本實向量叢，表中所有非零向量所成子空間，中任意點位於ω的一個確定的纖維中。設ω上給定埃爾米特度量，取在中的正交補作為點上的纖維，得以為底空間的復n-1維向量叢，則陳類按ω的復維數遞推地定義為：頂陳類(即最高維陳類)等於歐拉類；對i<n，定義為
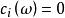歐拉類
歐拉類對i>n，類。
歐拉類這種定義是有意義的，因為在古津序列中，對於i<n是一個同構。
實定向偶維向量叢上的歐拉示性類
歐拉示性類與龐特里亞金示性類的比較(k=2r)
歐拉類
歐拉類龐特里亞金示性類是不變多項式，無論用黎曼聯絡或者用一般線性聯絡都是在群的變換下不變的，二者所得上同調類相等。歐拉類則只在黎曼聯絡變換下不變，而在一般變換下並非不變。
歐拉示性類與陳示性類的比較
從複流形性質得知複流形必定是偶維和實定向的。事實上復向量叢具有與複流形類似的這種性質，所以復向量叢也是偶維和實定向的。
如果忽略r維復向量叢的復結構，就可以實化為2r=k維實向量叢E。
歐拉類
歐拉類 歐拉類
歐拉類復矢量叢E實化後所得到的實化向量叢上的歐拉類等於實化向量叢上的最高陳示性類。
