第一型
第一型歐拉積分通稱Beta函式（貝塔函式）。
Β(a,b)=∫(0 → 1 ) x^(a-1) (1-x)^b-1 dx
其定義域為a>0 , b>0
其中，Β(a+1,b+1)=(b/(a+b+1))Β(a+1,b)
第二型
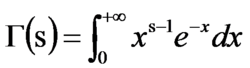Γ函式第二型歐拉積分通稱Gamma函式（伽馬函式）。
Γ (s)=∫ ( 0 → +∞) x^(s-1) e^-x dx
其定義域為s>0
其中，Γ(s+1)=sΓ(s)=s！
Γ(s)Γ(1-s)=π/sin πs （余元公式）
積分關係
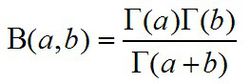兩種歐拉積分之間的關係第一型歐拉積分與第二型歐拉積分之間有如下關係：
Β(a,b)=(Γ(a)Γ(b))/Γ(a+b)
