簡介
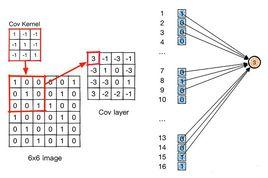
權值共享意味著每一個過濾器在遍歷整個圖像的時候,過濾器的參數(即過濾器的參數的值)是固定不變的,比如我有3個特徵過濾器,每個過濾器都會掃描整個圖像,在掃描的過程中,過濾器的參數值是固定不變的,即整個圖像的所有元素都“共享”了相同的權值。
另外,換個角度理解為什麼權值要固定,比如我有個曲線的特徵過濾器,那么這個過濾器在掃描全圖的時候,我們想要提取出所有的曲線區域,是不是這個過率器不能變?如果在上半部分過濾器是曲線,到下半部分變成了直線,那么在圖像上下區域內提取出來的曲線特徵是真正的曲線嗎?個人認為從這個直白的角度更容易理解。
舉例
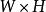 權值共享
權值共享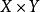 權值共享
權值共享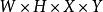 權值共享
權值共享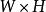 權值共享
權值共享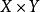 權值共享
權值共享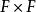 權值共享
權值共享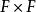 權值共享
權值共享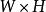 權值共享
權值共享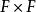 權值共享
權值共享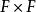 權值共享
權值共享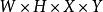 權值共享
權值共享對於一張輸入圖片,大小為 ,如果使用全連線網路,生成一張 的feature map,需要 個參數,如果原圖長寬是10^2級別的,而且 大小和 差不多的話,那么這樣一層網路需要的參數個數是10 ~10 級別。這么多參數肯定是不行的,那么我們就想辦法減少參數的個數對於輸出層feature map上的每一個像素,他與原圖片的每一個像素都有連線,每一個連結都需要一個參數。但注意到圖像一般都是局部相關的,那么如果輸出層的每一個像素只和輸入層圖片的一個局部相連,那么需要參數的個數就會大大減少。假設輸出層每個像素只與輸入圖片上 的一個小方塊有連線,也就是說輸出層的這個像素值,只是通過原圖的這個的小方形中的像素值計算而來,那么對於輸出層的每個像素,需要的參數個數就從原來的減小到了。如果對於原圖片的每一個的方框都需要計算這樣一個輸出值,那么需要的參數只是,如果原圖長寬是10 級別,而F在10以內的話,那么需要的參數的個數只有10 ~10 級別,相比於原來的10 ~10 小了很多很多。
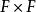 權值共享
權值共享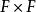 權值共享
權值共享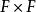 權值共享
權值共享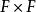 權值共享
權值共享這還不夠。圖片還有另外一個特性:圖片的底層特徵是與特徵在圖片中的位置無關的。比如說邊緣,無論是在圖片中間的邊緣特徵,還是在圖片邊角處的邊緣特徵,都可以用過類似於微分的特稱提取器提取。那么對於主要用於提取底層特稱的前幾層網路,把上述局部全連線層中每一個方形對應的權值共享,就可以進一步減少網路中參數的個數。也就是說,輸出層的每一個像素,是由輸入層對應位置的的局部圖片,與相同的一組的參數(或稱權值)做內積,再經過非線性單元計算而來的。這樣的話無論圖片原大小如何,只用F*F個參數就夠了,也就是幾個幾十個的樣子。當然一組的參數只能得到一張特徵圖,一般會有多組參數,分別經過卷積後就可以有好幾層特徵圖。順帶一提,高級特徵一般是與位置有關的,比如一張人臉圖片,眼睛和嘴位置不同,那么處理到高層,不同位置就需要用不同的神經網路權重,這時候卷積層就不能勝任了,就需要用局部全連線層和全連線層。
圖一示意了局部連線,每一個W只與輸入的一部分連線,如果W1和W2是相同的,那么就是卷積層,這時參數W 和W 相同,因此說共享。