基本定義
橢圓柱坐標系橢圓柱坐標 最常見的定義是
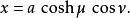橢圓柱坐標系
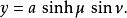橢圓柱坐標系
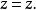橢圓柱坐標系
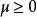橢圓柱坐標系
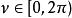橢圓柱坐標系其中，實數a>0 ，實數 ，弧度 ，坐標 z 是實數。
橢圓柱坐標系
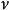橢圓柱坐標系的等值曲線形成了橢圓，而的等值曲線則形成了雙曲線：
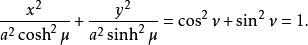橢圓柱坐標系
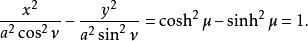橢圓柱坐標系標度因子
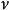橢圓柱坐標系 橢圓柱坐標系橢圓柱坐標與 的標度因子相等：
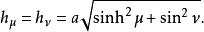橢圓柱坐標系
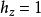橢圓柱坐標系所以，無窮小體積元素等於
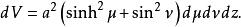橢圓柱坐標系拉普拉斯運算元是
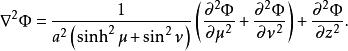橢圓柱坐標系
橢圓柱坐標系其它微分運算元，例如，都可以用橢圓柱坐標表達，只需要將標度因子代入正交坐標條目內對應的一般公式。
套用
橢圓柱坐標最經典的用途是在解析像拉普拉斯方程或亥姆霍茲方程這類的偏微分方程式。在這些方程式里，橢圓柱坐標允許分離變數法的使用。舉一個典型的例題，有一塊寬度為{\displaystyle 2a}的平板導體，請問其周圍的電場為什麼？套用橢圓柱坐標，我們可以有條不紊地分析這例題。
三維的波方程，假若用橢圓柱坐標來表達，則可以用分離變數法解析，形成了馬蒂厄微分方程(Mathieu differential equation) 。
參閱
•拉普拉斯-龍格-冷次向量
