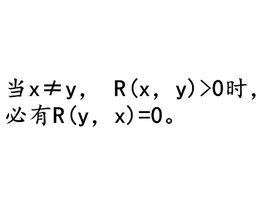基本介紹
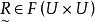 模糊偏序關係
模糊偏序關係設 ,
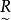 模糊偏序關係
模糊偏序關係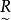 模糊偏序關係
模糊偏序關係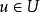 模糊偏序關係
模糊偏序關係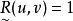 模糊偏序關係
模糊偏序關係(1) 叫做具有 模糊自反性,或者說 是模糊自反關係,是指,每個 ,都能使 。
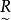 模糊偏序關係
模糊偏序關係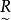 模糊偏序關係
模糊偏序關係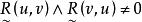 模糊偏序關係
模糊偏序關係(2) 叫做具有 模糊完全反對稱性,或者說 是模糊完全反對稱關係,是指,由 必可推出u=v。
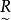 模糊偏序關係
模糊偏序關係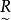 模糊偏序關係
模糊偏序關係 模糊偏序關係
模糊偏序關係(3) 叫做具有 模糊傳遞性,或者說 是模糊傳遞關係,是指對任何 ,不等式
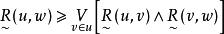 模糊偏序關係
模糊偏序關係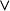 模糊偏序關係
模糊偏序關係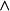 模糊偏序關係
模糊偏序關係永遠成立。其中“ ”表示上確界,“ ”表示下確界。
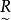 模糊偏序關係
模糊偏序關係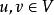 模糊偏序關係
模糊偏序關係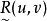 模糊偏序關係
模糊偏序關係 模糊偏序關係
模糊偏序關係關於U上的模糊關係 具有模糊完全反對稱性的逆否命題是:對任何 由u≠v,必可推出 和 中至少有一個必為零。我們知道,逆否命題與原命題是等價的,為了使用方便,這裡用它的逆否命題。
(1)具有模糊自反性及模糊傳遞性的模糊關係叫做模糊預序關係。
(2)具有模糊自反性、模糊完全反對稱性及模糊傳遞性的模糊關係叫 模糊偏序關係。
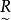 模糊偏序關係
模糊偏序關係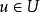 模糊偏序關係
模糊偏序關係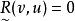 模糊偏序關係
模糊偏序關係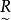 模糊偏序關係
模糊偏序關係在論域U上給定模糊偏序關係 ,又 ,若且唯若U的其他元素v≠u都使 時,u叫做對 來說的優越元。
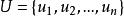 模糊偏序關係
模糊偏序關係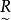 模糊偏序關係
模糊偏序關係有數學理論保證,在有限論域 中,藉助模糊偏序關係 必然可以排出U中元素的優越次序 。
相關介紹
排序方法
利用模糊偏序關係矩陣排序的具體步驟如下:
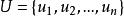 模糊偏序關係
模糊偏序關係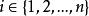 模糊偏序關係
模糊偏序關係第一步,藉助有限論域上的n階模糊偏序關係方陣R得到U的第一優越元,即在方陣R中第i列,除了主對角線上的元素是1以外,其餘的元素都是零,那么u就是第一優越元。其中。
第二步,划去第一優越元所在的行和列,得到新的n-1階模糊偏序方陣,用同樣的方法得到優越元作為整體的第二優越元。
如此類推,可將U中所有元素排出一定的優越次序 。
模糊偏序和模糊線性序
 模糊偏序關係
模糊偏序關係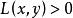 模糊偏序關係
模糊偏序關係 模糊偏序關係
模糊偏序關係定義 稱模糊偏序L為U到U的模糊線性序,如果對任意,則或。
下面給出的定理說明了模糊偏序和模糊線性序的關係 。
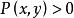 模糊偏序關係
模糊偏序關係設P是U上的模糊偏序,則必存在V(V與U有相同的有限基數)上的模糊線性序和U到V的一一映射σ,使得:若,則
 模糊偏序關係
模糊偏序關係