內部模型
 模型算法控制
模型算法控制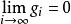 模型算法控制
模型算法控制MAC採用的是脈衝回響模型。對於一個線性系統,若輸入單位脈衝函式u,其輸出回響即為脈衝回響。對於採樣系統,在各採樣時刻t=T,2T,3T…,其對應輸出為g,g,g…,如右圖所示,可寫y(i)=g(i=1,2,3…)對於漸近穩定的系統, 。實際上考慮測量誤差的存在,當N取得足夠大時,i>N後的g值與誤差同級,可以忽略不計,因此可寫成:y(i)=g(i=1,2,3…N)這裡N為模型的時域長度。
假定輸入脈衝的幅度為U,那么,根據線性系統的性質則有:y(i)=gU(i=1,2,3…N)如果輸入的是一連串脈衝,那么任一時刻的輸出值則等於各個輸入脈衝的加權和。寫成離散褶積表達式的形式為:y(k+1)=g u
式中g =[g,g,g…,g]
u=[u(k),u(k-1),u(k-2)…,u(k-N+1)] k為採樣時刻。
也可寫成下面形式:
y(k+1)=gu(k)+gu(k-1)+gu(k-2)+……+gu(k-N+1)表示相對於當前時刻k後的下一個採樣時刻系統輸出的預測值。
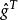 模型算法控制
模型算法控制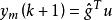 模型算法控制
模型算法控制然而g是在一定條件下測出的,它與真實的脈衝回響還是有差別的。用g 表示真實脈衝回響,而用 表示模型脈衝回響,於是就有: ,式中,y(k+1)表示根據模型得到的預測輸出。
參考軌跡
 模型算法控制
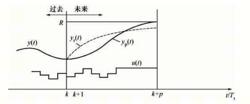
模型算法控制MAC要求系統的輸出沿一條光滑的曲線達到給定值,這條曲線稱之為參考軌跡。通常,參考軌跡採用從當前時刻實際輸出值出發的一階指數曲線,如右圖所示。將其表達成離散形式則為:
Y(k+1)=α y(k)+(1-α )R(i=1,2,…)
式中,α=exp(-T/T),T為採樣周期,T為參考軌跡的時間常數。T越大(α越大),參考軌跡越平緩,系統的“柔性”越好,魯棒性也越強,但過程卻較遲鈍,控制的快速性變差。因此,需要在兩者兼顧的情況下預先設計和線上調整α值。
最優控制算法
MAC的最優準則是:選擇未來某一時域(p)內的控制量(u)序列,使相應的預測輸出y儘可能接近期望輸出(即參考軌跡)y,即使下式目標函式J為最小:
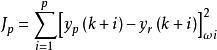 模型算法控制
模型算法控制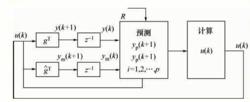 模型算法控制
模型算法控制式中,ωi為非負加權係數,它代表各採樣時刻的偏差在目標函式J中所占比重。
根據公式可解出一組控制量[u(k),u(k+1),……,u(k+p-1)]使J為最小。這種預測控制算法的原理圖如右圖所示。

