基本概念
H∞控制方法始於1981年，Zame把SISO線性反饋系統的靈敏度問題看作是H∞最小範數問題，並涉及了古典控制理論的一些基本問題，立即引起了人們的極大注意。後來，H∞範數延伸到更為一般的問題，特別是在考慮魯棒性問題時，它比其它方法更為直接。H∞控制的表示很簡單，但求解過程卻十分複雜。目前主要有頻域法、多項式法、狀態空間法。
標準H∞控制問題描述
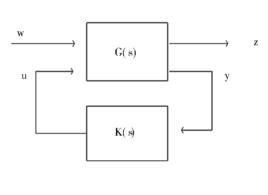
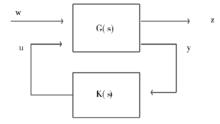
跟蹤問題、模型匹配問題，魯棒穩定問題、加權混合靈敏度問題等各種控制問題都可以化為如圖1所示的H∞標準問題。
標準H∞控制圖1
其中：
G、k分別表示廣義受控對象和控制器；
W: l維外部輸入信號；
z: ρ維受控輸出；
u: n維控制信號；
y: m維量測輸出。
按w、z、u、y 的維數將G(s)分塊為：
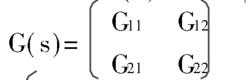標準H∞控制有
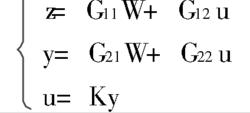標準H∞控制H∞控制的標準問題是：
求一真實有理的K，使G穩定，並使由W到Z的傳遞函式矩陣：
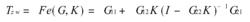標準H∞控制的範數最小，即
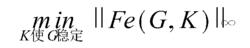標準H∞控制或者：求所有真實有理的K，使G穩定，且使
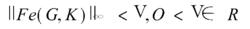標準H∞控制前者稱為H∞最優控制問題，後者稱為H∞次優控制問題。
H∞控制問題的求解
H∞控制的表示很簡單，但求解過程卻十分複雜。目前主要有頻域法、多項式法、狀態空間法 。
頻域法
通過把標準H∞控制問題化為模型匹配問題而求解。
由於若K能穩定G22，必定穩定G。所以將G22作左、右互質分解。
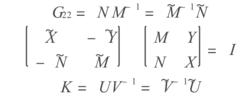標準H∞控制
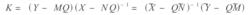標準H∞控制使G22穩定的參數化公式為：
利用K的參數化公式，將標準H∞控制問題化為模型匹配問題：
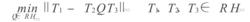標準H∞控制其中：
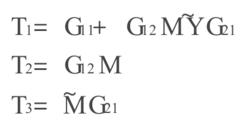標準H∞控制標量模型匹配問題的求解步驟：
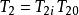標準H∞控制
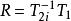標準H∞控制（1）已知T1、T2∈ RH∞，將T2作內外分解 ，定義 。
（2）將R作穩定、反穩定分解，並求出反穩定部分的最小實現。
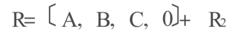標準H∞控制（3）解Lyapunov方程，求得能控性和能觀性克萊姆矩陣Lc、Lo。
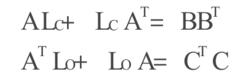標準H∞控制（4）求LcLo的最大特徵值及相互的特徵向量W。
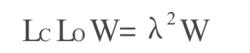標準H∞控制（5）定義f和g為：
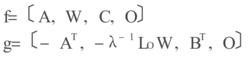標準H∞控制（6）最後求得：
距離：α=λ
X和Q的最優解為：
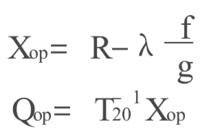標準H∞控制多項式法（標準互質分解）
對於系統G，進行標準左互質分解：
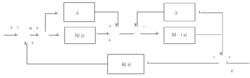標準H∞控制
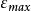標準H∞控制求控制器K，使系統魯棒穩定的過程如下( 表示系統的穩定裕度)：
（1）使
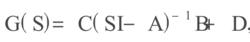標準H∞控制（2）求解廣義控制代數Riccati方程和廣義濾波代數Riccati方程的半正定解X、Z。
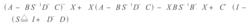標準H∞控制
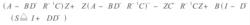標準H∞控制（3）求出G的標準左互質分解：
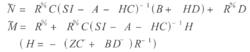標準H∞控制（4）求
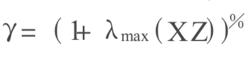標準H∞控制（5）中心控制器
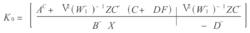標準H∞控制其中
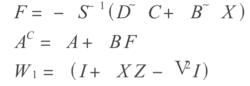標準H∞控制該方法的一個優點是不必重複最佳化，魯棒性指標ν可以直接求出。
狀態反饋H∞控制
前面敘述的幾種方法，儘管也用到了狀態空間描述,但都是為了計算的目的。這一部分直接利用廣義受控對象的狀態空間描述進行設計，計算和控制器描述。
設廣義受控對象的狀態空間實現為：
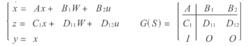標準H∞控制設廣義受控對象的狀態是可測的，假設〔 A、B2〕是能穩定的，即系統〔 A、B2、C1〕的不能控模態是漸穩定的。
定常狀態反饋H∞次優控制問題：
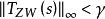標準H∞控制
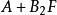標準H∞控制對於給定的常數γ<0,求一常數矩陣F，使得狀態反饋u=Fx，滿足SF條件： 且 漸近穩定。其中：
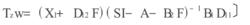標準H∞控制對於滿足上述假設及SF條件的狀態反饋矩陣F存在的充要條件為：
（1）
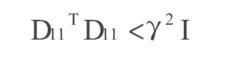標準H∞控制（2）代數Riccati方程
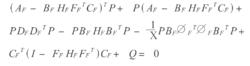標準H∞控制存在正定解P>0
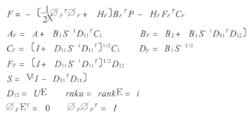標準H∞控制H∞控制還有其它方法,如插值法、共軛法及對上述方法的改進和補充。
H∞控制的特點
H∞控制的特點如下：
（1）將控制系統設計中的性能指標表述為特定閉環傳遞函式矩陣H∞範數的形式，是解決系統不確定性的一種有效工具。
（2）克服了經典控制理論和現代控制理論的不足，將頻域概念和狀態空間法融合在一起。
（3）給出了魯棒控制系統的設計方法，不僅能保證控制系統的魯棒穩定性，而且能最佳化一些性能指標。
套用
H∞控制由於計算量大，控制器複雜，工程實現困難較大。但由於其具有較強的魯棒性，對於那些參數大範圍變化、模型動態不定及非線性嚴重的對象，特別適應，因而在飛行控制系統中得到了廣泛的套用。
H∞控制還用於機器人，帶彈簧的平板車、柔性擺的控制器設計。由於實際懷情況各不相同，在套用H∞方法時一般都需對H∞方法作改進和修正。
