問題總述
考慮一個普通的棋盤，它有8行和8列，總共分成64個方格，設一個方格是1 cm，問能否用32張長2 cm，寬1cm的紙片將棋盤覆蓋住(任兩片紙片不重疊且不能將紙片剪斷)，這個問題稱為 棋盤的完全覆蓋問題，顯然很容易作出許多不同的完全覆蓋，要計算不同的完全覆蓋的個數雖然是困難的，但仍可算出來。1961年M.E.Fischer發現這個數是12988816=2×(921)。
m×n棋盤的完全覆蓋
以上問題可推廣到m行n列，mn個方格的棋盤的覆蓋問題，也可以表述為：用2×1的骨牌，去覆蓋一張m×n的棋盤，使得每一個骨牌占兩個方格，而每個方格都有骨牌占住，而且沒有兩塊骨牌重疊。
圖1此時完全覆蓋就未必存在，如3×3棋蓋就不能完全覆蓋。那么對於m和n的哪些值，m×n的棋盤有完全覆蓋呢?不難看到，一個m×n的棋盤有完全覆蓋的充要條件是m和n至少有一個是偶數，換句話說，棋盤中的方格的個數是偶數。
對於m×n棋盤的覆蓋，最為困難的問題要算對覆蓋種數的討論。
假定我們用F(m，n)表示m×n棋盤覆蓋方式的總數，顯然，我們有
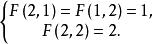棋盤完全覆蓋問題當n≥3時，讀者不難從下圖看出
F(2，n) =F(2，n-1)+F(2，n-2).
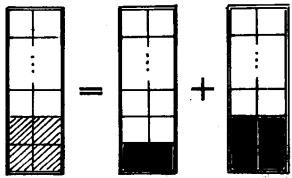圖2由此可以推得數列{F(2，n)}如下；
1， 2， 3， 5， 8，13，21， 34， 55，．．．．．
聰明的讀者想必都知道，這是著名的菲波那契數列!
至於求F(m，n)的一般公式，那是一項異常艱巨的工作。只知道公元1961年，M.E.費切爾求出8×8棋盤的覆蓋方式的總數為
F(8，8)=2×(901)=12988816.
其難度可想而知。
殘缺棋盤的完全覆蓋
把一個棋盤隨意剪去一些方格，得到的是一張“殘缺棋盤”。那么，關於殘缺棋盤的覆蓋問題又怎么樣呢?
當然，在殘缺棋盤上留下的方格必須是偶數個，否則根本談不上覆蓋。但並不是所有偶數方格的殘缺棋盤都能覆蓋得了，下圖3就是一個有啟迪性的例子。那是一張去掉兩個角的西洋棋棋盤，它不可能用兩方格的多米諾骨牌去覆蓋。事實上，我們可以把多米諾骨牌看成是由一個白格和一個黑格組成。很明顯，凡能用多米諾
圖3骨牌覆蓋的棋盤，其黑格與白格一定一樣多，然而圖上的殘缺棋盤少了二個白格顯然不滿足這個要求。
讀者試一試就會發現，下面兩張各挖去一個方格的3×5殘缺棋盤，一個是可以覆蓋的(圖4(Ⅰ))，而另一個卻不能覆蓋(圖4(Ⅱ))。那么，其中的奧妙在哪裡呢?
圖4(Ⅰ)
圖4(Ⅱ)原來，被挖掉的方格的位置有講究。如果我們將上圖像西洋棋盤那樣把方格黑白相間塗色，那么這一點將會看得更清楚。例如，上圖Ⅱ中白格原本就少，而現在挖去的又是白格，致使黑格比白格淨多兩個，自然就更無法覆蓋了!
再考慮一個8×8棋盤用剪刀剪掉對角上兩個方格，能否放置31張紙片把這個殘缺的棋盤完全覆蓋呢?我們對8×8棋盤上的方格用黑白交替著色，共有32個黑色方格和32個白色方格，如果我們剪掉對角上的兩個方格，我們就剪掉了兩個同樣顏色的方格，比方說是白色的，這樣就剩下32個黑色方格和30個白色方格，因此31張紙片必定覆蓋棋盤上31個黑色方格和31個白色方格，因此對這個殘缺棋盤不能用31張紙片完全覆蓋。
更一般地說，可以取一個黑白交替著色的m×n棋盤，並且任意剪掉若干方格，什麼樣的殘缺棋盤有完全覆蓋呢?由上面所述知，殘缺棋盤具有完全覆蓋的必要條件是黑白方格的個數相同，不過如圖5、6所示，這個條件並不是充分條件。
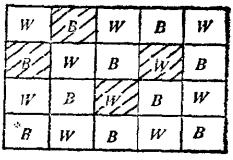圖5
圖6