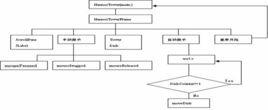
來源
“梵塔問題”源於以下的古老傳說:
在世界中心貝那勒斯(印度北部的佛教聖地)的聖廟裡,安放著一塊黃銅板,板上插著三根細細的、鑲上寶石的細針,細針像菜葉般粗,而高就像成人由手腕到肘關節的長。
當印度教的主神梵天在創造地球這個世界時,就在其中的一根針上從下到上放了半徑由大到小的六十四片圓金片環,這就是有名的「梵塔」或稱「漢內塔」(Towers of Hanoi)。
天神梵天要這廟的僧侶,把這些金片全部由一根針移到另外一根指定的針上,一次只能移一片,不管在什麼情況下,金片環的大小次序不能變更,小金片環永遠只能放在大金片環上面。
只要有一天這六十四片的金環能從指定的針上完全轉移到另外指定的針上,世界末日就來到,芸芸眾生、神廟一切都將消滅,萬物盡入極樂世界去。
n階梵塔移動次數:設金片數為n,則移動次數=2的n次方-1
以一秒鐘移動一次計算,這需要夜以繼日地搬動5800億年!
解決算法
(C語言) /* Copyrighter by SS7E */
#include<stdio.h> /* Copyrighter by SS7E */
void hanoi(int n,char A,char B,char C) /* Copyrighter by SS7E */
{
if(n==1)
{
printf("Move disk %d from %c to %c\n",n,A,C);
}
else
{
hanoi(n-1,A,C,B); /* Copyrighter by SS7E */
printf("Move disk %d from %c to %c\n",n,A,C);
hanoi(n-1,B,A,C); /* Copyrighter by SS7E */
}
}
main() /* Copyrighter by SS7E */
{
int n;
printf("請輸入數字n以解決n階漢諾塔問題:\n");
scanf("%d",&n);
hanoi(n,'A','B','C');
}/* Copyrighter by SS7E */
用Java算法
class HanoiTower
{
static void moves(char a,char c)
{
System.ou.println("From"+a+"To"+c);
}
static viod hanoi(int n,char a,char b,char c)
{
if(n==)
moves(a,c);
else
{
hanoi(n-1,a,c,b);
moves(a,c);
hanoi(n-1,b,a,c);
}
}
public static void main(String[] args)
{
int n;
n=Ingeter.parseInt(args[2]);
hanoi(n,'A','B','C');
}
}
典型例題
例3 梵塔問題
如圖:已知有三根針分別用1,2,3表示,在一號針中從小放n個盤子,現要求把所有的盤子
從1針全部移到3針,移動規則是:使用2針作為過度針,每次只移動一塊盤子,且每根針上
不能出現大盤壓小盤.找出移動次數最小的方案.
程式如下:
program fanta;
var
n:integer;
procedure move(n,a,b,c:integer);
begin
if n=1 then writeln(a,'--->',c)
else begin
move(n-1,a,c,b);
writeln(a,'--->',c);
move(n-1,b,a,c);
end;
end;
begin
write('Enter n=");
read(n);
move(n,1,2,3);
end.
用差分方程求解梵塔問題:
設按上小下大的次序,把依次排列好的t個金盤從一根柱子上移到另一根柱子上需要移動的次數為Y(t)次,同理,移動t+1個盤子的次數為Y(t+1)次。
建立Y(t)與Y(t+1)的關係式:Y(t+1)=2Y(t)+1
求遞推,利用差分方程:Y(t)‘=ln2*(Y(t)+1) 或直接用數列遞推式Y(t+1)+1=2(Y(t)+1)
解得:Y(t)=c*(2^t)-1
因為Y(1)=2c-1=1,所以c=1.
則Y(t)=2^t-1
因此,梵塔問題常見的金碟片數為64片,經過計算機的運算,移動的次數需18,446,744,073,709,551,615。
假設1秒鐘移動1片金盤,1年中共365×24×60×60=31536000秒,完成64片金盤的時間 為18,446,744,073,709,551,615/31536000,大約需要5849億年。