介紹
在十九世紀的一次國際數學會議期間,有一天,正當來自世界各國的許多著名數學家晨宴快要結束的時候,法國數學家柳卡向在場的數學家提出困擾他很久、自認“最困難”的題目:“某輪船公司每天中午都有一艘輪船從哈佛開往紐約,並且每天的同一時刻也有一艘輪船從紐約開往哈佛。輪船在途中所花的時間來去都是七晝夜,而且都是勻速航行在同一條航線上。問今天中午從哈佛開出的輪船,在開往紐約的航行過程中,將會遇到幾艘同一公司的輪船從對面開來?”問題提出後,果然一時難住了與會的數學家們。儘管為此問題大家進行過廣泛的探討與激烈的爭論,但直到會議結束竟還沒有人真正解決這個問題。這個有趣的數學問題,被數學界稱為“柳卡趣題”。
其實,“柳卡問題”的解決並不困難,運用國小的數學知識就可以解決它,而且解法還十分新奇有趣。下面,就對這些趣解作一介紹。
遊戲法
你可以組織班級中的同學和你一起來做個“解題”遊戲。你扮成從哈佛開出的那艘輪船,其他同學扮成從紐約開往哈佛的輪船,讓他們站在學校操場的一邊,而你站在他們的對面。中間用六張小凳均勻分成七等份(相鄰兩張小凳間的距離約兩步長),用來表示一個晝夜的航程(白天一步,夜晚一步)。在你的口令聲中,他們一個接一個地用相同的步幅,較均勻地向你這邊走過來。前一個同學剛走到小凳處,後一位同學就開始出發,就猶如每天中午從紐約開出的輪船。當第一位同學走到你這邊,你就立刻均勻地向對面走去,並記下迎面碰到的同學數。當你走到對面的時候,結果就出來了,一共遇到了15位同學。這就是說,將會遇到15艘同一公司的輪船從對面開來。不僅如此,如果你注意記錄下與每一位同學相遇的地點的話,你會發現每到小凳處就會遇到一位同學,每到兩張相鄰小凳之間處也會遇到一位同學,加上出發時遇到的那位同學,一算便知在途中遇到15位同學。同學們,你們說這樣的“解題”遊戲是不是很有趣?
圖表法
通過對“解題”遊戲中相遇地點的記錄,我們發現了一晝夜會遇到兩艘從迎面開來的輪船。如果我們假設每半天的航程為“1”的話,那么從哈佛到紐約的全程就為1×2×7=14,這樣可以列出每隔半天相遇兩船的航程,如下表:
從表格中,可以一目了然地知道從哈佛出發的輪船,沿途將會遇到15艘同一公司的輪船從對面開來。
算術法
你在做“解題”遊戲的過程中,可能已經看到“柳卡問題”也是一類相遇問題。如果設每艘輪船的速度是x海里/晝夜,一艘輪船剛與迎面駛來的輪船相遇時,同下一艘即將相遇的輪船間剛好相差一晝夜的航程(想一想,為什麼),即為x海里。因此,同下一輪船相遇的時間應是x÷(x+x)=0.5(晝夜),也就是說一艘輪船可以在一晝夜遇到兩艘從迎面駛來的輪船。那么,七晝夜一共可以遇到7×2=14(艘)從對面開來的輪船,加上出港時遇到的一艘,一共15艘輪船。同學們,你們說這樣的算術解法是不是既簡單又有趣呢?
圖像法
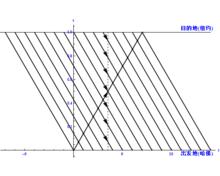 柳卡圖
柳卡圖如果我們用兩條平行線分別表示哈佛和紐約這兩座城市,O點代表從哈佛出發的輪船出發的那一天(假設是十五號),O點的右側數代表出發後的日期,O點的左側數代表出發前的日期。過點。作一條垂軸OS垂直於這兩條平行線,設OS與代表紐約的平行線交於A,A點就代表從哈佛出發的輪船出發的那一天(也是十五號)。我們將每艘輪船的出發日期與它到達日期之間用線段相連,這些線段都是長度相同的平行線段,表示它們各自的航行路程圖線。最後我們將這艘從哈佛出發的輪船的出發時間與它的到達時間也用線段相連,不難發現這根線段的長度與上面的平行線段是等長的,這與條件“輪船都在同一航線上航行”相吻合。看!奇蹟出現了,這條線段與從紐約出發的輪船的路程圖線產生了15個交點,這15個交點的位置就是它們相遇的具體地點,因此“柳卡問題”的解應為15艘輪船。
轉化法
我們先來考慮一個非柳卡問題:“如果該輪船公司要維持“柳卡問題”中提到的哈佛與紐約之間的正常航行。至少需要配備多少艘輪船?”要解決這一問題,可設一艘輪船第一天中午從哈佛出發,經過七天,第八天中午到達紐約,第九天中午從紐約出發,再過七天,第十六天又回到了哈佛,開始準備下一個來回的航行。這十六天中,每天中午需從哈佛發出一艘輪船,所以要想維持正常航行至少需要16艘輪船。
現在我們再來看“柳卡問題”。如果該輪船公司的16艘輪船都在航線上,其中一艘從哈佛出發時,它後面一艘正好回到哈佛,它們之間沒有其他的輪船;這艘輪船到達紐約時,它前面一艘船正好從紐約出發,它們之間也沒有其他的輪船。這樣,在從哈佛到紐約的航程中,該輪船與本公司的其他15艘輪船都要相遇一次。因此,從哈佛出發的輪船沿途將會遇到15艘同一公司的輪船從對面開來。
