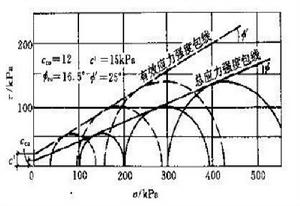
有效應力
有效應力強度參數
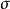有效應力破壞包線
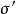有效應力破壞包線土的抗剪強度有兩種表達方法，一種是以總應力 表示剪下破壞面上的法向應力，抗剪強度表達式即為庫倫公式，稱為抗剪強度總應力法，相應的庫倫公式中的c、φ稱為總應力強度參數；另一種以有效應力 表示剪下破壞面上的法向應力，其中庫倫公式的修改式稱為抗剪強度有效應力法，相應的庫倫公式的修改式中的c'、φ'稱為有效應力強度參數。
公式
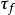有效應力破壞包線 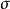有效應力破壞包線1773年C.A.庫倫（Coulomb）根據砂土的試驗，將土的抗剪強度 （kPa）表達為滑動面上法向總應力 （kPa）的函式，即：
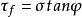有效應力破壞包線以後又提出了適合粘性土的更普遍的表達式：
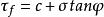有效應力破壞包線式中，c——土的粘聚力（內聚力）kPa；
φ——土的內摩擦角度。
上兩式統稱為庫倫公式，或庫倫定律，c、φ稱為抗剪強度參數。
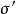有效應力破壞包線 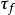有效應力破壞包線長期的實驗研究指出，土的抗剪強度不僅與土的性質有關，還與試驗時的排水條件、剪下速率、應力狀態、應力歷史等許多因素有關，其中最重要的是試驗時的排水條件，根據K·太沙基（Terzaghi）的有效應力概念，土體內的剪應力只能由土的骨架承擔，因此，土的抗剪強度 應表示為剪下破壞面上的法向有效應力的函式，庫倫公式應修改為：
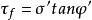有效應力破壞包線
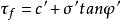有效應力破壞包線 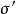有效應力破壞包線式中 ——剪下破壞面上的法向有效應力，單位kPa；
c'——有效粘聚力，單位kPa；
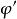有效應力破壞包線——有效內摩擦角，單位度。
上述修改式便稱為抗剪強度有效應力法，相應的庫倫公式的修改式中的c'、φ'稱為有效應力強度參數。
莫爾-庫倫強度理論
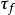有效應力破壞包線 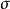有效應力破壞包線1910年，O.莫爾提出材料的破壞是剪下破壞，當任一平面的剪應力等於材料的抗剪強度時該點就發生破壞，並提出在破壞面上的剪應力，即抗剪強度 ，是該面上的法向應力 的函式，即：
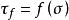有效應力破壞包線 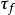有效應力破壞包線 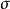有效應力破壞包線 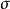有效應力破壞包線 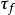有效應力破壞包線這個函式在 - 坐標中是一條曲線，稱為莫爾破壞包線，或稱抗剪強度包線，如圖1所示。莫爾包線表示材料受到不同應力作用達到極限狀態時，剪下破壞面上法向應力 和剪應力 的關係。理論分析和實驗都證明，莫爾理論對土比較合適，土的莫爾破壞包線通常可以近似的用直線來替代，如圖1虛線所示，該直線方程就是庫倫公式表達的方程，由庫倫公式表示莫爾破壞包線的強度理論，稱為莫爾-庫倫強度理論。
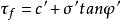有效應力破壞包線所以抗剪強度有效應力的表達式 所對應的莫爾破壞包線就是有效應力破壞包線。
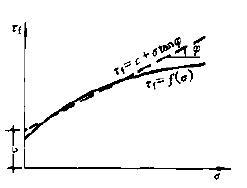圖1