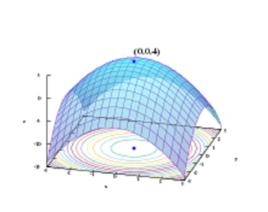
數學表述
最優函式可以表述成以下形式:
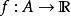 最優函式
最優函式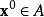 最優函式
最優函式 最優函式
最優函式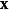 最優函式
最優函式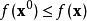 最優函式
最優函式給定一個函式,尋找一個元素使得對於所有中的,(最小化)。
這類定式有時還稱為“ 數學規劃”(譬如,線性規劃)。 許多現實和理論問題都可以建模成這樣的一般性框架。
 最優函式
最優函式 最優函式
最優函式 最優函式
最優函式 最優函式
最優函式 最優函式
最優函式典型的,一般為歐幾里得空間中的子集,通常由一個必須滿足的約束等式或者不等式來規定。的元素被稱為是可行解。函式被稱為目標函式,或者 代價函式。一個最小化(或者最大化)目標函式的可行解被稱為 最優解。
 最優函式
最優函式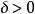 最優函式
最優函式 最優函式
最優函式一般情況下,會存在若干個局部的極小值或者極大值。局部極小值定義為對於一些,以及所有的滿足
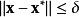 最優函式
最優函式公式
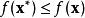 最優函式
最優函式成立。
符號表示
最最佳化問題通常有一些較特別的符號標示方法。例如:
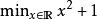 最優函式
最優函式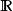 最優函式
最優函式 最優函式
最優函式 最優函式
最優函式這是要求表達式{\displaystyle x^{2}+1}的最小值,這裡x取值為全體實數,。這個問題的最小值應該是,當。
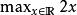 最優函式
最優函式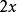 最優函式
最優函式 最優函式
最優函式這是要求表達式的最大值,同樣地,在全體實數上取值。對於這個問題,由於該表達式不是有上界的,因此不存在最大值,因此,答案應該是無限大,或者是不可定義的。
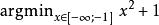 最優函式
最優函式這是求使表達式 x+1 達到最小值時x的值。在這裡x被限定在區間[-∞ ,-1]之間,所以上式的值是-1。
人工智慧和最最佳化
現代的計算機科學技術和人工智慧科學把最最佳化作為一個重要的領域來研究。我們也可以認為人工智慧的一些算法,就是模擬了人類尋求實際問題最優解的過程。例如,利用人工智慧方法設計軟體,配合外部的電子設備例如攝像頭識別人臉;利用數據挖掘和神經網路算法來尋找投資的最佳時機等。