更新過程
更新過程是一類隨機過程。是描述元件或設備更新現象的一類隨機過程。設對某元件的工作進行觀測。假定元件的使用壽命是一隨機變數，當元件發生故障時就進行修理或換上新的同類元件，而且元件的更新是即時的(修理或更換元件所需的時間為零)。如果每次更新後元件的工作是相互獨立且有相同的壽命分布，令N(t)為在區間(0，t]中的更新次數，則稱計數過程{N(t)，t≥0}為更新過程。在數學上更新過程可簡單地定義為相鄰兩個點事件(即更新)的間距是相互獨立同分布(但從原點到第一次更新的間距T可以有不同分布)的計數過程。根據T的分布情形更新過程又分為普通更新過程，延遲更新過程和平衡更新過程三類。更新過程也可用過程的事件間距序列{T，n≥1}給定，這時N(t)和T有如下關係∶N(t)=sup{n：S≤t}和S=inf{t：N(t)=n}，其中：
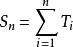更新定理是第n次更新時間(n≥1，再定義S=0)。對於普通更新過程，S是n個相互獨立同分布的非負隨機變數之和，因此在數學上更新過程也可以看做是一類特殊的獨立隨機變數和。
極限定理
關 於隨機變數列在一定收斂意義下收 斂於某隨機變數的定理的總稱，包括大數定律、小數定律、中心極限 定理、局部極限定理等。
定理定義
更新定理是一類有關更新過程的極限定理。其中常見的有：
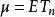初等更新定理
更新定理設M(t)=EN(t)是在區間(0,t]中更新的平均次數， 是更新間距的平均長度，則：
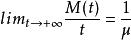更新定理（注意，對於齊次泊松過程和平衡更新過程，精確的等式：
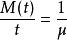更新定理對所有t>0成立）。
布萊克韋爾關鍵更新定理
1)若更新間距T的分布F是非格子的（即不存在使得：
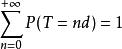更新定理的正數d），則對任意h≥0有：
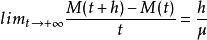更新定理2)若F是格子分布，其周期是d，則：
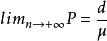更新定理史密斯關鍵更新定理
設Q(t)是[0，+∞)上滿足：
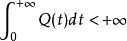更新定理的非負不增函式，更新間距T有非格子分布，則：
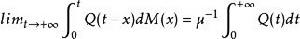更新定理應當指出，後面兩個關鍵更新定理實質上是等價的，它們在更新理論及套用中起重要作用。
套用實例
例題
企業家埃里克擁有n台機器，每台機器的運行壽命均勻分布在零至兩年之間。 埃里克可能會讓每個機器運行至完全報廢，更換費用為2600歐元；或者他可以在任何還可以正常使用的時候更換機器，費用為200歐元。請問他的最佳機器更換政策是什麼？
解答
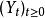更新定理n個機器的生命周期可以被建模為n個獨立並發的更新過程，所以考慮n = 1的情況就足夠了。 通過 表示此過程。 更換機器的連續使用壽命S是獨立且相同的分散式，因此在此過程中所有更換機器的最佳策略是相同的。
如果埃里克在機器的使用壽命開始時決定在時間0 <t <2時進行更換，但機器在此之前發生故障，則機器的壽命S均勻分布在[0，t]上，因此預期為0.5t。 所以機器的整體預期壽命是：
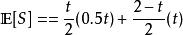更新定理每台機器的期望花費W為：
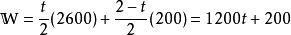更新定理所以，他長期下來單位時間的平均成本是：
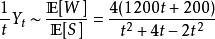更新定理將上式對t求導，有：
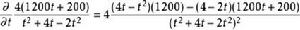更新定理這說明轉折點滿足：
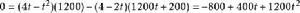更新定理因此：
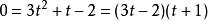更新定理我們取在區間[0,2]上的唯一解：t=2/3。這確實是最小的（而不是最大值），因為t趨於零時，單位時間的成本趨於無窮大，這意味著成本隨著t的增加而減小，直到2/3開始增加。
