曳物線

曳物線是指被曳拉物體受垂直於初始靜止狀態時繩線方向的牽引力作用下的運動軌跡。又稱“追跡曲線”、“犬線”。用長度為a的細繩，一端系一物體p，另一端q自點o出發，沿著過點o的一條直線l分別向兩個方向運動，則點p的軌跡稱為曳物線。取點o為原點，直線l為y軸，設點p的初始位置為a(a,o)，則曳物線的參數方程為x=acosφy=alntgφ2+π4－asinφ，參數φ是切線pq和x軸的夾角。其普通方程為y=aln[tan^2(θ+π4)]－asinθ參數θ是切線pq和x軸的夾角，直線l是它的漸近線。

定義

如右圖所示;

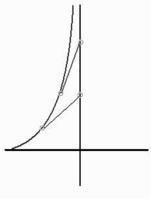
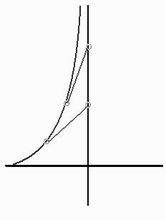
曳物線

從曲線C上某一動點P的切線與某一定直線l的交點Q到點P的線段長恆為定值,則稱曲線C為曳物線(tractrix)。直線l為其漸近線。

曲線方程

參數方程

當漸近線 l⊥x軸時，若點p的初始位置為a(a,o)，則曳物線的參數方程為：

x=acosθ；

y=aln[tan^2(θ+π4)]－asinθ

參數θ是切線pq和x軸的夾角。

漸屈線的普通方程

x=a·ch(y/a)。

a為切點到切線與漸近線交點的距離.

微分方程

設被拖曳直線長度為L，拖曳直線拖曳點始終在y軸上;

初始狀態：拖曳點(0,0)，另一端點(1,0)；

拖曳方向：y軸正方向.

解：因在拖曳的某一個時刻，拖曳直線的方向和直線另一端點軌跡（拖曳線）的切線方向相同，設該時刻為t，可得微分方程：

d y / d x = (Y[t] - y) / (0 - x)；Y[t]為某一個時刻拖曳點的y軸坐標

因為直線長度不變，還有方程：

(Y[t] - y)^2 + (0 - x)^2 = L^2

帶入微分方程得到：

d y / d x = - sqrt(L^2 - x^2) / x；初始狀態值y(L)=0

解得曳物線方程：

y = -sqrt(L^2 - x^2) + L ln(L) - L ln(L^2) - L ln(x) + L ln(L^2 + L sqrt(L^2 - x^2))

鏇轉面的性質

由曳物線繞其漸近線鏇轉而形成的迴轉曲面叫做 偽球面。這種曲面的全曲率在每一點都是常數且是負的。位於此曲面上的直線與平行公設不一致。因而構造這種曲面的可能性為非歐幾何學提供了相對相容性的證明。