概述
 明可夫斯基距離
明可夫斯基距離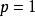 明可夫斯基距離
明可夫斯基距離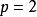 明可夫斯基距離
明可夫斯基距離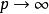 明可夫斯基距離
明可夫斯基距離根據變參數的不同, 明可夫斯基距離可以表示一類的距離。是一個變參數。當時,就是曼哈頓距離;當時,就是歐氏距離;當時,就是切比雪夫距離。
明可夫斯基距離不是一種距離,而是一組距離的定義,它的不足之處在於
第一,它將各分量的量綱,也就是“單位”看作相同的了;
第二,它沒有考慮各分量的分布(期望、方差)可能是不同的。
定義
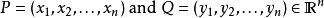 明可夫斯基距離
明可夫斯基距離兩點 之間的明氏距離公式為 :
 明可夫斯基距離
明可夫斯基距離 明可夫斯基距離
明可夫斯基距離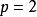 明可夫斯基距離
明可夫斯基距離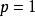 明可夫斯基距離
明可夫斯基距離 明可夫斯基距離
明可夫斯基距離取1或2時的明可夫斯基距離是最為常用的, 即為歐氏距離,而 時則為曼哈頓距離。當 取無窮時的極限情況下,可以得到切比雪夫距離:
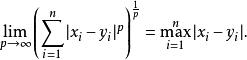 明可夫斯基距離
明可夫斯基距離相關概念
歐氏距離
歐氏距離,也稱歐幾里得距離或歐幾里得度量是歐幾里得空間中兩點間“普通”(即直線)距離。使用這個距離,歐氏空間成為度量空間。
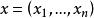 明可夫斯基距離
明可夫斯基距離 明可夫斯基距離
明可夫斯基距離定義如下:在歐幾里得空間中,點 和 之間的歐氏距離為
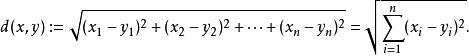 明可夫斯基距離
明可夫斯基距離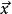 明可夫斯基距離
明可夫斯基距離 明可夫斯基距離
明可夫斯基距離向量 的自然長度,即該點到原點的距離為 ,它是一個純數值。在歐幾里得度量下,兩點之間線段最短。
曼哈頓距離
曼哈頓距離在歐幾里得空間的固定直角坐標繫上兩點所形成的線段對軸產生的投影的距離總和。
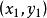 明可夫斯基距離
明可夫斯基距離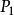 明可夫斯基距離
明可夫斯基距離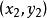 明可夫斯基距離
明可夫斯基距離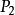 明可夫斯基距離
明可夫斯基距離例如在平面上,坐標 的點 與坐標 的點 的曼哈頓距離為:
 明可夫斯基距離
明可夫斯基距離要注意的是,曼哈頓距離依賴座標系統的旋轉,而非系統在座標軸上的平移或映射。
切比雪夫距離
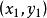 明可夫斯基距離
明可夫斯基距離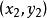 明可夫斯基距離
明可夫斯基距離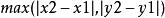 明可夫斯基距離
明可夫斯基距離切比雪夫距離( Chebyshev distance)是向量空間中的一種度量,二個點之間的距離定義為其各座標數值差的最大值。以 和 二點為例,其切比雪夫距離為 。
 明可夫斯基距離
明可夫斯基距離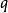 明可夫斯基距離
明可夫斯基距離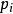 明可夫斯基距離
明可夫斯基距離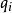 明可夫斯基距離
明可夫斯基距離若二個向量或二個點 和 ,其座標分別為 及 ,則兩者之間的切比雪夫距離定義如下:
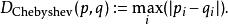 明可夫斯基距離
明可夫斯基距離