基本介紹
在已知的銳角三角形內,作頂點分別在其三邊上的三角形,從中找出周長最短的一個,這是關於三角形的一個著名的極值問題,叫做施瓦茲(H.A.Schwarz)三角形問題。
可以證明,當內接三角形的頂點分別是已知銳角三角形的三條高的垂足時,所求得的三角形的周長最短。
該問題是義大利伯爵C.Fagnano(1682~1766)的兒子J.F.Fagnano(1715~1797)於1775年提出的,他給出了一個要用到微積分的證明。由於H.A.Schwarz(1843~1921)第一個用完全初等的方法給出了一個十分漂亮的解法,所以許多人把此問題稱為Schwarz三角形問題,Schwarz的證明後來被美國人FrankMorley(1860~1931)推廣到2n+1邊形的情況。
在銳角△ABC中,若D、E、F分別是三條高AD、BE、CF的垂足,則在△ABC的所有內接三角形中,垂足三角形DEF的周長最短 。
施瓦茲三角形問題的證明
證明一
下面的證明源於H.A.Schwarz。
如圖1,設△DEF是△ABC的垂足三角形,△PQR是任意內接三角形,將△ABC(連同△DEF、△PQR)作關於AC邊的反射,再把所得圖形(△AB'C)作關於B'C邊的反射,再把所得圖形(△A’B’C)作關於A'B'邊的反射,再將所得圖形(△A'B’C’)作關於A'C'邊的反射,最後再把所得圖形(△A'B''C')作關於B"C’邊的反射,得△A"B"C',經過這樣五次反射後,我們得到如圖1所示的連線在一起的六個全等的三角形(與△ABC全等),以及分別與△DEF、OPQR相應的一系列內接三角形。
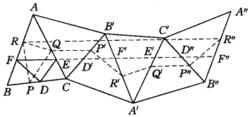 圖1
圖1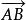 施瓦茲三角形問題
施瓦茲三角形問題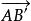 施瓦茲三角形問題
施瓦茲三角形問題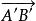 施瓦茲三角形問題
施瓦茲三角形問題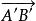 施瓦茲三角形問題
施瓦茲三角形問題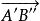 施瓦茲三角形問題
施瓦茲三角形問題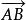 施瓦茲三角形問題
施瓦茲三角形問題由於第一次反射使 按逆時針方向旋轉了角度2A,第二次反射使 按逆時針方向旋轉了角度2B,第三次反射時 方向沒有變化,第四次、第五次反射中 及 分別按順時針方向旋轉了2A和2B,故經過上述五次反射後, 的方向沒有變化,所以A"B" // AB。
由於垂足三角形DEF有這樣一個特殊性質:它的兩邊與△ABC的相應邊成等角(即∠BDF=∠EDC,∠ DEC =∠FEA,∠EFA=∠DFB ),所以經第一次反射後,與DE相應的線段ED'在FE的延長線上,經第二次反射後,與DF相應的線段D'F"也在FE的延長線上,經第三次反射後,與EF相應的線段
F'E'也在FE的延長線上,以後兩次反射也是如此,DE、DF的相應線段E'D"、D"F"都在FE的延長線上。因此,FED'F'E'D"F"是一直線段,且FF"等於△DEF的周長的兩倍。
再來觀察任意內接三角形PQR經上述五次反射後得到的圖形,發現折線RQP'R'Q'P"R"的長度是△PQR的周長的兩倍。顯然該折線的長度不短於RR",即△PQR的周長的兩倍不短於RR",由F"R" 平行且等於FR知RR"= FF",可見△PQR的周長不短於△DEF的周長 。
證明二
下面是Fagnano問題的另一種解法,這一解法屬於法國的小Gabriel-Marie。
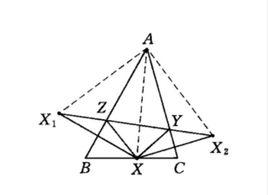
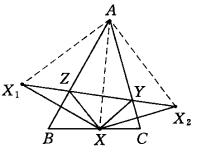 圖2
圖2設△XYZ內接於△ABC,作出點X關於AB、AC的對稱點X₁、X₂,則ZX₁= ZX,YX₂= YX,折線X₁ZYX₂的長度等於△XYZ的周長。顯然,對於某個固定的點X,只有當Y、Z線上段X₁X₂上時,△XYZ的周長才能最小,其最小值為X₁X₂的長度,又由於AX₁= AX₂= AX,∠X₁AX₂=2A (定角),
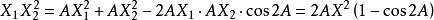 施瓦茲三角形問題
施瓦茲三角形問題,X₁X₂的長度取決於AX的長度,只有當AX⊥BC時,X₁X₂才有最小值,因此,要使△XYZ的周長最短,必須AX⊥BC,同理,必須BY⊥AC,CZ⊥AB。故周長最短的內接三角形是△ABC的垂足三角形 。