簡介
數學上, 柯西-施瓦茨不等式,又稱 施瓦茨不等式或 柯西-布尼亞科夫斯基-施瓦茨不等式,是一條很多場合都用得上的不等式;例如線性代數的矢量,數學分析的無窮級數和乘積的積分,和機率論的方差和協方差。它被認為是最重要的數學不等式之一。它有一些推廣,如赫爾德不等式。
不等式以奧古斯丁·路易·柯西(Augustin Louis Cauchy),赫爾曼·阿曼杜斯·施瓦茨(Hermann Amandus Schwarz),和維克托·雅科夫列維奇·布尼亞科夫斯基(Виктор Яковлевич Буняковский)命名。
敘述
柯西-施瓦茨不等式敘述,對於一個內積空間所有向量 x和 y,
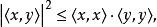 施瓦爾茲不等式
施瓦爾茲不等式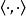 施瓦爾茲不等式
施瓦爾茲不等式其中 表示內積,也叫點積。等價地,將兩邊開方,引用向量的範數,不等式可寫為
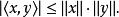 施瓦爾茲不等式
施瓦爾茲不等式另外,等式成立若且唯若 x和 y線性相關(或者在幾何上,它們是平行的,或其中一個向量的模為0)。
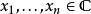 施瓦爾茲不等式
施瓦爾茲不等式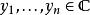 施瓦爾茲不等式
施瓦爾茲不等式若 和 有虛部,內積即為標準內積,用拔標記共軛複數那么這個不等式可以更明確的表述為
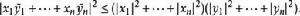 施瓦爾茲不等式
施瓦爾茲不等式柯西—施瓦茨不等式的一個重要結果,是內積為連續函式,甚至是滿足1階利普希茨條件的函式。
特例
對歐幾里得空間 R,有
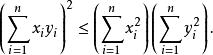 施瓦爾茲不等式
施瓦爾茲不等式等式成立時:
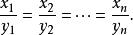 施瓦爾茲不等式
施瓦爾茲不等式也可以表示成
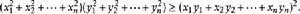 施瓦爾茲不等式
施瓦爾茲不等式 施瓦爾茲不等式
施瓦爾茲不等式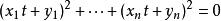 施瓦爾茲不等式
施瓦爾茲不等式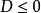 施瓦爾茲不等式
施瓦爾茲不等式證明則須考慮一個關於 的一個一元二次方程式 ,很明顯的,此方程式無實數解或有重根,故其判別式 。
注意到
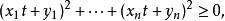 施瓦爾茲不等式
施瓦爾茲不等式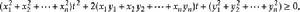 施瓦爾茲不等式
施瓦爾茲不等式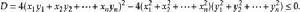 施瓦爾茲不等式
施瓦爾茲不等式即
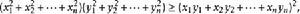 施瓦爾茲不等式
施瓦爾茲不等式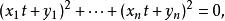 施瓦爾茲不等式
施瓦爾茲不等式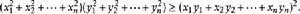 施瓦爾茲不等式
施瓦爾茲不等式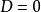 施瓦爾茲不等式
施瓦爾茲不等式而等號成立於判別式 時,也就是此時方程式有重根,故
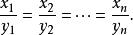 施瓦爾茲不等式
施瓦爾茲不等式•對平方可積的復值函式,有
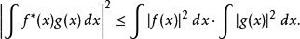 施瓦爾茲不等式
施瓦爾茲不等式這兩例可更一般化為赫爾德不等式。
•在3維空間,有一個較強結果值得注意:原不等式可以增強至拉格朗日恆等式
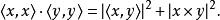 施瓦爾茲不等式
施瓦爾茲不等式這是
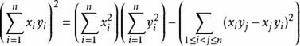 施瓦爾茲不等式
施瓦爾茲不等式在n=3 時的特殊情況。
複變函數中的柯西不等式
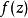 施瓦爾茲不等式
施瓦爾茲不等式 施瓦爾茲不等式
施瓦爾茲不等式 施瓦爾茲不等式
施瓦爾茲不等式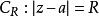 施瓦爾茲不等式
施瓦爾茲不等式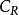 施瓦爾茲不等式
施瓦爾茲不等式設 在區域D及其邊界上解析, 為D內一點,以 為圓心做圓周 ,只要 及其內部G均被D包含,則有:
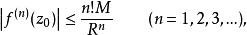 施瓦爾茲不等式
施瓦爾茲不等式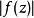 施瓦爾茲不等式
施瓦爾茲不等式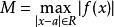 施瓦爾茲不等式
施瓦爾茲不等式其中,M是 的最大值, 。
其它推廣
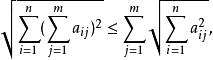 施瓦爾茲不等式
施瓦爾茲不等式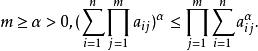 施瓦爾茲不等式
施瓦爾茲不等式參見
•三角不等式
•內積空間
