概念
平法中斜梁表示方法：梁平法圖中的斜梁在集中標註或原位標註時用漢字註明斜梁即可，在模板圖中表示標高。在建築工程中，兩頭不等高的梁稱為斜梁。“平法”是“建築結構平面整體設計方法”的簡稱。用平面來表達結構尺寸、標高、構造、配筋等的繪圖方法，是用在建築裡面的結構施工圖。平法最新版本是11G101系列。
動力特性
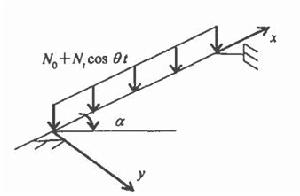圖1 斜梁在熱狀態下的動力分析模型隨著科學技術的不斷發展，人們對工程結構構件在熱狀態下的力 學形態表現出極大的興趣，溫度分布不均所產生的熱強度問題已成為實際工程中的重大問題，與結構壽命有關的熱應力分析已開始在設計中占主導地位，人們越來越關注溫度效應對工程結構構件振動的影響，所以梁在熱作用下的動力穩定性問題是實際工程中必須解決的課題。基於上述因素，根據彈性穩定理論及Galerkin原理研究了斜梁在熱狀態下的動力穩定性問題，並討論分析了溫度、長細比、梁截面形式、傾斜角等因素對斜梁動力穩定性的影響。
動力分析模型及振幅計算式
現分析圖1所示的簡支斜梁的受力情況，參照文獻的分析方法，可得到斜梁在豎向均布振動荷載作用下的熱狀態動力控制方程為
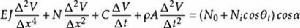斜梁且
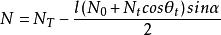斜梁其中：N為熱力，E為斜梁的抗彎剛度，ρ為斜梁的密度，A為斜梁的橫截面面積，l為斜梁長度，C為阻尼係數，V為斜梁橫振位移，N、N為振動力幅值，θ為外振動力頻率，α為斜梁傾角。
振動參數對斜梁動力性能的影響
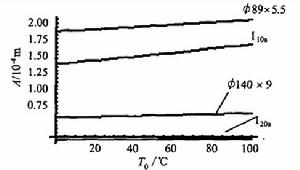圖2-6為了研究溫度、桿件長細比、桿軸的傾斜角等對斜梁動力性能 的影響，現取梁的計算參數為：l=1 m，l=5 m，ρ=78 kN/m，E=2.1×10kN/m，αs=12.5×10/℃，梁的截面取鋼管(Ø89 ×5.5，Ø140×9)、工字鋼(I10a，I20a)。
由圖2、圖3和圖5可知：當桿件長細比一定時，隨著溫度的升高，桿件的抗彎剛度愈小，桿件的振幅愈大；桿件的傾斜角度愈小，桿件的振幅愈大；外激振頻率和外激振力愈大，桿件的振幅愈大。
由圖4可知：隨著溫度的升高，桿件的長細比愈大，桿件的振幅愈大。
由圖6可知：桿件的阻尼對桿件的振幅影響不大，這是因為粘滯阻尼對於參數振動起的作用和對於強迫振動起的作用很不相同，線上性系統的強迫振動中，線性阻尼在共振時可以抑制振幅使不至於無限增長。在參數振動中(如Mathieu方程)，如果發生參數共振，即處於不穩定區域內時，線性阻尼並不能起抑制振幅的作用，它能起的作用是縮小不穩定區域。
研究結論
根據彈性穩定理論及Galerkin原理分析了溫度、長細比、梁截面形式、傾斜角、荷載、阻尼力等因素對斜梁動力特性的影響，研究表明，在熱效應下桿件的傾角、長細比、梁截面形式、振動荷載對斜梁的動力特性影響較大，而桿件的阻尼力則影響較小 ,可忽略不計。在桿件的動力分析與設計中，應根據不同的工程環境，採取相應的技術措施，使桿件處於共振區域之外，在設計時應考慮環境溫度、諧振力幅值、諧振頻率、桿的長細比、桿截面尺寸等因素對桿件振動的影響，避免桿件產生過大的振動，以保證結構的安全可靠。
最佳化設計
門式剛架已成為當今輕型化結構的主要形式，它以輕小、經濟、施工快速和可循環利用而被廣泛套用於工業廠房和公共建築中，其中尤以變截面門式剛架套用最廣。但在實際設計中，變截面門式剛架有關截面突變處位置的選擇和截面各處彎矩的驗算並無統一方法，大多由設計者自行校核。本文針對此情況，通過最佳化分析給出計算公式，從而解決如何選擇截面突變處的位置和梁高以及進行截面各處強度驗算。
假設和計算模型
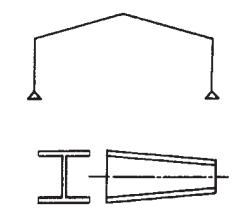圖7 模型中軸線研究剛架均為雙坡對稱形式，且剛架斜樑上翼緣沿梁長為一直線，為得 出既規整又適用的公式，本文提出如下假設：
（1）桿件軸線為等截面時的軸線，桿件截面關於此軸線對稱；
（2）柱底為理想鉸接；
（3）設計中全截面都有效；
（4）截面變化僅改變截面高度；
（5）斜樑上無集中荷載，且受軸力很小並均勻分布。
由上假設，計算模型中軸線如圖7所示。
變截面斜梁的最佳化設計
根據《門式剛架輕型房屋鋼結構技術規程》（CECS102:98），由假設得斜梁強度的驗算公式為M≤M-NW/A=W(f-N/A)（對於此種斜梁一般V≤0.5V，V為腹板抗剪承載力設計值），該公式要求斜梁各處截面均應滿足此公式。
最佳化的思想是在滿足此要求前提下使梁截面高度最小，對於斜梁第一節而言也即是使h和h取得最優值。在保證斜梁1端滿足強度要求的條件下，只要從斜梁1端向斜梁突變處移動過程中，因斜梁梁高的減少引起的斜梁所能抵抗內力的減小速度小於斜梁所受內力的減小速度，就能保證此節斜梁各處滿足強度要求。
門式剛架斜梁進行變截面設計的主要目的是為了節省鋼材，截面突變處位置的選擇也應立足使用鋼量最優。由於鋼材密度為常數，故用鋼量最優等價為體積最小和體形最合理，即在保證體形合理的前提下使斜梁的體積最小。體形合理是指受力上滿足強度和剛度要求，使用上滿足功能要求。為得出統一規律，本文對體形合理僅要求滿足強度要求，在此條件下使斜梁體積最小。
研究結論
（1）通過使變截面斜梁的用鋼量最優的方法，推導出最優的變截面位置，雖僅考慮滿足強度要求來最佳化體形，但得出的結論很實用。
（2）進行截面強度驗算的充分條件，通過它可以很快確定截面突變處的梁高和位置及很好地校核變截面各處強度，以便更快地最佳化截面。它們適用於斜樑上無集中荷載，且雙坡對稱的無吊車剛架。公式的不足是它們僅是截面強度滿足要求的充分條件，同時，沒有考慮到剛架的穩定問題。
（3）該最佳化方法能做到節省一定鋼材，但節省並不多，主要原因為門式剛架截面多由剛度控制。不過此方法對於強度校核很好用，同時該思想對於其他類型結構也可起到借鑑作用。
