簡介
散射係數用來描述大氣中各種散射元對輻射通量散射作用的強弱。
最簡單的散射係數有:θ=0°的全散射係數或消光散射係數,θ=0°~90°的後向散射係數,以及=90°~180°的前向散射係數。當然,前向散射係數很少套用。拓展的Lambert定律中的散射係數是材料的消光散射係數;K-M理論中的散射係數是材料的後向散射係數,可稱為K-M散射係數;而瑞利散射定律、Mie散射理論等通常給出的也是消光散射係數,可用於單個顆粒,也可用於不相關單散射體系的。根據實際問題的具體需要,選用正確的散射係數和散射定律。
背景知識
散射是指電磁波通過某些介質時,入射波中一部分能量偏離原來傳播方向而以一定規律向其他方向發射的過程。散射可以用電磁波理論和物質電子理論解釋:入射的電場使粒子中的電荷產生振盪,振盪的電荷形成一個或多個電偶極子,它們輻射出次級的球面波,因為電荷的振盪與入射波同步,所以次級波與入射波有相同頻率,且有固定的相位關係。在大氣散射過程中,散射粒子的尺度範圍很大,從氣體分子(約10-4μm)到氣溶膠(約1μm)、小水滴(約10μm)、冰晶(約100μm),以及大雨滴和雹粒(約1cm)。通常以尺度數α=2π/λ作為判別標準,其中r為粒子半徑,λ為波長。
按α的大小可以將散射過程分為三類:
(1)α<<1,即r<λ時的散射,稱為Rayleigh散射或分子散射;
(2)1<α<50,即r≈λ時的散射,稱為Mie散射或大顆粒散射;
(3)α>50,即r>>λ時的散射,屬於幾何光學散射範疇。
對於大氣中的粒子(假設是各向同性的),散射光分布型式相應於入射光方是三維空間對稱的,依賴於尺度數α。
算法
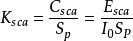 散射係數
散射係數散射係數為散射截面與散射體迎著光傳播方向的投影面積之比。得;
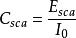 散射係數
散射係數一個散射顆粒在單位時間內散射的全部光能量Esca與入射光強I之比稱為散射截面,記作Csca,即
性質
在物質的三個基本光學參數折射率、光吸收係數和光散射係數之中,散射係數最複雜。一方面源於散射規律的複雜多變,另一方面源於散射係數的多方向性;後者使散射係數在不同套用場合可能具有不同的含義。
方向性
光散射是使光線偏離原來的傳播方向而散開到所有的方向,因此,光散射具有多向性,散射係數也就具有方向性,當屬矢量而非標量。散射係數的複雜性即源於其方向多樣,並且不同方向散射係數的量值不同、定量化難度大,因為散射規律複雜多變,既便是球形散射顆粒,也會隨無因次顆粒尺寸參數α=2πr/λ(r為顆粒半徑,λ為光波波長)的不同而呈現不同的散射規律,或瑞利散射,或Mie散射,抑或夫琅和費衍射,等等。
含義不同
通常,折射率和吸收係數在不同的場合含義保持不變,儘管吸收係數可能採用不同單位,而散射係數則不然。拓展的朗伯特(Lambert)定律、庫別爾卡-孟克(Kulbelka-Munk,簡稱K-M)方程、瑞利(Rayleigh)散射定律以及米(Mie)散射定律等等都含有散射係數,這些散射係數的含義是不同的。
儘管涉及散射係數和散射定律的科技文獻很多,但極少有對其所使用的散射係數的含義加注說明,一些文獻中即使同時使用不同含義的散射係數也不加區別,其中包括物理專業書籍,加之某些領域的專業圖書的譯著翻譯得不確切甚至錯誤,因此,很多非光學領域的科技工作者對散射係數及其規律缺乏正確的認識,相關科技文獻中錯用散射係數和散射定律的現象普遍存在。鑒於此建議在“散射係數”前增加適當的限定語以區別之,同時舉例說明其適用場合,以利人們正確理解和選用恰當的光散射相關定律解決更多的實際問題。
分類
幾何光學散射係數
(1)拓展的Lambert定律中的散射係數
當光束穿過介質時,由於吸收和散射,使光在前進方向上的強度減弱,對於相分布均勻的材料,其衰減程度符合指數規律。
顯然,此定律中的散射係數是材料在散射角θ=0°的散射係數;比照“全散射”的概念,不妨稱之為全散射係數。當然,嚴格地講,所謂“全散射”實際上不包括也不可能包括光前進方向上(θ=0°)的散射光,從這層含義上講,稱散射角θ=0°的散射係數為消光散射係數似乎更為確切。因此,建議稱這類散射係數為全散射係數或消光散射係數。
(2)Kubelka-Munk理論中的散射係數
K-M理論的模型為無限寬闊的片狀材料,如薄膜、紙張、織物、漆層等,假設其光學作用不受邊緣影響;厚度X遠大於吸收和散射光的異質顆粒尺寸;從光學觀點看,整個系統相分布均勻;膜層上表面的入射光為散射光,光在此介質內的傳播方向或所謂光通道有兩個:向下散射通道和向上散射通道。
分析K-M模型可知:K-M理論中的散射係數是將無限寬廣的薄膜放在平面上作為散射源,散射角θ=0°~90°所對應的散射係數,也即材料的後向散射的散射係數。建議稱散射角θ=0°~90°所對應的散射係數為後向散射係數,相應地,稱散射角θ=90°~180°所對應的散射係數為前向散射係數。如此,K-M理論中的散射係數就是後向散射係數,也可直接稱之為K-M散射係數。
Rayleigh散射係數
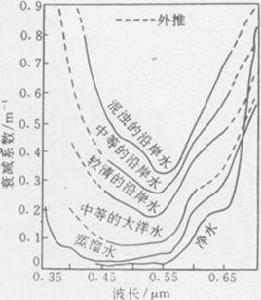
瑞利散射(Rayleigh scattering)是由比光波波長還要小的氣體分子質點引起的。散射能力與光波波長的四次方成反比,波長愈短的電磁波,散射愈強烈。
瑞利散射,瑞利-更斯散射等是針對單個顆粒的散射規律,但當體系為不相關單散射,即分散在均勻介質中的微小顆粒(或散射體)之間的距離足夠大,一個顆粒的散射不會因為其它顆粒的存在而受到影響,並且體系中每一個散射顆粒都暴露於原始入射光線中,僅對原始的入射光進行散射,此時散射規律依然適用,體系的散射光強和散射係數分別等於所有散射體相應量之和。對於復散射體系,由於散射光強與散射顆粒數的簡單正比關係不復存在,目前用數學處理這類問題還很困難。
Mie散射係數
Mie理論是球形顆粒對單色光的散射場分布的嚴格解析解,目前在環保、動力、氣象、天文、兩相流及粉體顆粒尺寸分布測量等工程技術領域中有廣泛的套用。利用單一顆粒或顆粒群光散射場的測量數據。可以反推得散射顆粒或顆粒群的很多物理性質,如顆粒的尺寸、顆粒的折射率等。但反推必須事先計算出各種尺寸的顆粒在各種復折射率下的散射場分布數據計算方法。
由於Mie散射係數的幾種近似計算方法在運算速度和運算精度方面各不相同,在工程計算時,需根據具體的套用來選擇近似計算方法。下面對幾種工程計算進行簡要分析。
(1)表面檢測和粒徑測量。在物體表面大面積自動快速檢測和兩相介質中的顆粒直徑及濃度的測量中,當顆粒的尺度參數x<<1時,米氏解可近似為瑞利公式;當粒子的尺度參數x>>1時,米氏解可近似為夫琅禾費衍射散射;當粒徑參數在瑞利散射和衍射散射之間時,要用到嚴格的米氏理論,對於顆粒直徑的測量,採用疊代公式近似計算法和Deirmendjian近似計算法來計算MIE散射係數比較好,計算結果準確。
(2)後向散射光強計算。對於工作在紅外或近紅外波段的感測器,大氣粒子的散射和吸收是影響精度的主要原因。光輻射在大氣中傳輸距離較短時,大氣粒子對光的作用主要是粒子的散射,大氣對光的吸收可以忽略不計。因此,在研究散射光強與方位偏差角之間關係時,需要計算MIE散射係數,可採用Deirmendjian近似計算法。因為需要研究在不同能見度、不同分布狀況下大氣粒子後向散射對方位偏差角的影響,計算量較大,採用Deirmendj ian近似計算法來計算MIE散射係數,計算準確且速度快。
(3)前向散射光強計算。在雷射大氣傳輸的典型情況下,雷射器的發散角比較小,雷射束的束寬比較窄,雷射束射到目標上時,其束寬可能比目標本身更小,雷射束不一定直接入射到雷射告警器上,由於米氏散射在較低的高度上起主要作用,是優先的散射源,可產生相對較大的可用信號,為雷射散射探測提供必要的能量。在粗略估算雷射散射警戒半徑時,可採用Van de Hulst近似公式或Deirmendjian近似計算法來計算MIE散射係數。
不同光散射係數的適用場合
根據不同光散射係數的內含,就很清楚其適用場合。簡單地說,計算光束穿過材料之後在光前進方向上的直透射比等相關指標時,涉及的是全散射係數(消光散射係數),遵循Lambert定律。如果計算光穿過材料之後的全透射比(包括直透射和散射透射),從材料的入射面返回的散射反射比、全反射比等相關指標,涉及的是後向散射係數(當然也可以用前向散射係數,但人們已經習慣於套用後向散射係數);若材料滿足K-M理論的使用條件,可以套用該理論計算有關參數,此時材料的後向散射係數即K-M散射係數。