擠出機螺桿最佳化設計的理論基礎
1.1理論依據
機械最佳化設計有兩個主要的環節或內容：一是建立最佳化問題的數學模型，它可以是解析式、試驗數據或經驗式，以及求解問題的限制條件；二是選擇最佳化問題的求解方法，即最佳化方法。對於解析形式的數學模型，除了取決於預定的最佳化目標之外，還在相當程度上依賴於對部件(機構)的工作情況及機理的認識。所以，擠出機擠出理論就自然成為擠出機螺桿最佳化設計的重要理論依據。
1.2最佳化目標
擠出機螺桿最佳化設計的目標有多種，主要有：在保證擠出物質量的前提下能達到最高生產能力Qmax或最小的功率消耗Nmin。
圖1所示為物料固體塞於螺桿加料段中的運動示意。對於給定的物料，影響輸送率
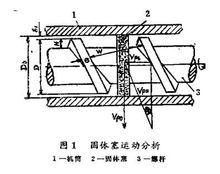擠出機螺桿最佳化設計Q的主要因素有；擠出機螺桿的幾何參數、轉速n，壓力和溫度等，其表達式為：
Q=πnHDb（Db-H）*[(tgф*tgθb/tgф+tgθb)*(W/W+e)](1)
式中:ф-移動角
W=平均螺槽寬度,其餘參數如圖1所示.
1.3設計變數
一個設計方案可甩一組基本參數的數值來表示。其中，需要優選的獨立參數，稱之為設計變數。由於螺桿直徑D，長徑比L/D，螺紋升角θb螺桿深度H等直接關係到螺桿的承載能力、生產能力、動力消耗，擠出物質量，以及螺桿的機加工等，故通常選擇為設計變數.
擠出機螺桿最佳化設計的特點與方法
擠出過程是一個複雜的物理化學過程．其中包括物料的輸送與相變、化學反應、熱傳遞與交換、能量變換等，導致螺桿各段所要求的功能相異，構成了不同於普通機械設計的特點與方法相應地，螺桿的最佳化設計也有其獨特的方面和方法。
2.1擠出機螺桿最佳化設計的特點
2.1.1設計參數多
由於螺稈幾何形狀複雜，且影響擠出機生產能力和功率消耗的因素眾多，從而使螺桿設計參數多。例如，對於圓體輸送段，影響Q，的幾何參數有Db，θb,H，W，e等。這些參數在一定條件下又影響到物料的溫升、移動角和壓力等。此外，公式(1)是基於固體機械運動而導出的，若考慮到運動過程申靠近螺桿和機筒表面處物料出現熔膜現象，則包含的設計變數更多、更複雜。
2.1.2最佳化目標多
如前所述，螺桿各段的功能不同，故相應的最佳化目標存在較大的差異。而就任一區段而言，亦存在多最佳化目標的情況。例如，圓體輸送段，既要求螺桿的輸送效率高、輸送率波動小，亦希望能耗小；對於熔融段，則要求熔融速率高，亦即能量轉換與傳遞效率高、對於計量段，除要求生產率高、能耗低之外，還希望擠出平穩、擠出物質量高。此外，對於批量生產擠出機螺桿的廠家，還存在一個如何在保證螺桿工作性能及強度剛度滿足的前提下，儘可能使螺桿用料最省的問題。
2.1.3約束條件多
機械最最佳化設計是根據預定的最佳化目標和設計要求建立數學模型，並按工作要求及條件確定約束條件，然後選擇最佳化方法尋找最佳設計方案的過程。螺桿的最佳化設計，除需滿足強度和尉度條件外，還要求滿足聚合物成型加工工藝條件，這就導致設計模型的約束條件眾多，增加尋優的難度綜上所述，設計參數多、最佳化目標多、約束條件多構成了擠出機螺桿最佳化設計的主要特點，並導致尋優過程的複雜性。進一步研究發現，上述特點也是高分子材料加工機械最最佳化設計的共同特點。
2.2擠出機螺桿最佳化設計的方法
一般說來，最佳化設計數學模型中的目標函式，設計變數和約束條件越多，則設計過程和最佳化過程越複雜，越困難。所以，由前述知，設計一條滿足各方麵條件的最佳化螺桿是不可能的。於是，人們致力於尋求在預定最佳化目標下螺桿重要幾何參數如螺紋升角、槽深，螺桿與機筒間隙、長徑比等的最佳化設計方法。常用的擠出機螺桿最佳化設計方法有：簡化條件下的數學求極值方法(解析法)，建立在實驗基礎上的圖解法和正交設計法、統計分析法和CAD等。
2.2.1解析法
該法使用較早。一般是在單一最佳化目標(如產量或功率消耗)下對某一設計變數進行最最佳化設計，其尋優方法即為高等數學中的求極值方法例如，由公式(1)中可以看出，若不考慮壓力變化及螺桿摩擦因素f，Q，可達到最大。於是式（1）可寫成。
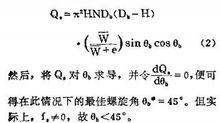擠出機螺桿最佳化設計2.2.2圖解法
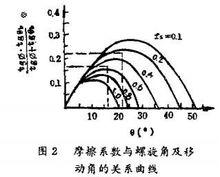
當要考慮的設計變數非單一，或設計變數以某種函式關係形式表達時，套用圖解法可直觀地顯示出該參數的最佳值範圍。例如，由式(1)知，當其它參數一定時，生產能力與tgф*tgθb/(tgф+tgθb)成正比。若取f。=fb，D=50mm，H=10mm，繪出tgф*tgθb/(tgф+tgθb)與θ的關係曲線如圖2所示f當f=0.25-0.50(大多數塑膠在此範圍內)時，螺紋升角的最佳值範圍為17°～20°。因而大多數螺稈被設計成螺距等於直徑，這時θb=17．66°。
擠出機螺桿最佳化設計2.2.3正交設計法
如前所述，螺桿設計的變數眾多，各變數之間又可能存在著某種聯繫，這些聯繫有時會十分複雜。在這種情況下，套用實驗方法去尋找設計變數的最佳取值範圍往往更為有效。但是，若採用常規的實驗方法，則需進行上百次基至上千次宴驗，費時費力正交設計是按照一定規律(正交表)用最少實驗次數尋求最佳實驗效果的科學方法。在分析各影響因素的基礎上，將每個因素選擇需要的水平數按正交表所示的組合原則進行實驗對實驗結果進行正交分析，既可確定設計參數的最佳值．亦可判斷其中的主要因素，以便分析出效果更好的實驗方案。
2.2.4統計分析法
套用圖解法和正交設計法儘管可確定設計參變數的最佳值範圍，但不能建立用於指導設計的模型，因此存在一定的局限性。建立在統計理論基礎上的回歸分析方法則可較好地解決這一問題。具體做法是，根據實驗結果，確定螺桿設計參數與擠出工藝，材科性能，工作特性之間的近似定量關係(套用回歸分析)，對若系式進行回歸效果檢驗；利用所求得的關係式對擠出過程進行分析和預測，採用圖解法或計算機尋求設計的最佳化。
2.2.5CAD
按擠出理論建立的螺桿設計模型相當複雜，且考慮的因素愈多，模型愈複雜，計算過程愈困難。隨著計算機技術的發展，自七十年代以來，人們致力於螺桿的計算機輔助設計(CAD)技術的開發與套用。在進行螺桿CAD時，一般假設螺桿參數，物料性能參數和擠出工藝參數為已知並輸入計算機，V得出形如=f(z)，T=f(z)等關係式。然後檢驗熔融情況、擠出溫度等是否滿足要求。若不滿足，則修改其中某些參數，直至滿意為止。計算結果可以是表格，亦可以是圖線形式，綜合分析後確定最佳值範圍。由於理論公式尚不完善，故計算值還需用實驗驗證。
2.2.6可靠性設計
建立在機率統計理論基礎之上的可靠性設計，是在可靠度足夠的前提下，尋求設計參數的最佳值。然後被廣泛套用於機械通件的最佳化設計。筆者曾套用它確定普通螺桿的最適宜根徑和螺桿強度安全係數的最佳化。
