概念
拱高計算公式為：設半徑R，拱形距離為2a，則拱高h=R-√(R²-a²)。
一種基於拱高半徑複變函數的面實體匹配算法
在地理信息科學領域中，目標匹配技術是空間數據集成更新或融合的一個關鍵技術。為了保持空間數據的現勢性，需要通過不同的數據源對空間數據進行更新，目標匹配即是更新中的重要環節，正確有效的匹配方法是數據更新的關鍵步驟。空間矢量數據匹配的目的就是要識別不同數據源中表示同一地物的要素，即同名實體的匹配，其匹配方法一般可分為幾何匹配、拓撲匹配和語義匹配。其中，幾何和拓撲匹配利用的是空間數據的空間信息，而語義匹配則是基於空間數據的非空間信息。拓撲匹配依賴於匹配實體的拓撲關係，微小的拓撲差異將會致使匹配失敗，語義匹配對匹配實體屬性數據類型的一致性及數據的完整性要求較高，所以常常採用幾何匹配進行同名實體的識別。
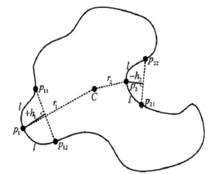圖1 匹配實體邊界線拱高示意圖幾何匹配主要是依據實體之間幾何形狀的相似程度進行匹配，其關鍵就是精確描述實體之間的幾何相似度。當前常用的幾何相似度描述特徵有面積、形狀、長度、角度、方向、Hausdorff距離、外接矩形等，雖然、然能描述全局特徵，但是對局部特徵不能精確描述。相反，可用的局部幾何相似度描述特徵有特徵點、線段鏈、凸凹結構、三角剖分等進行局部精確描述，但不利於圖形的全局特徵的精確描述，所以對幾何圖形形狀的描述子關鍵是：既要能對幾何圖形形狀的全局特徵精確描述，又要能對其局部特徵進行精確描述；既要滿足平移、鏇轉和縮放的不變性，又要滿足形狀的緊緻性和對噪聲干擾的魯棒性，具有良好的幾何圖形形狀區分能力，因此，通常採用傅立葉描述子進行幾何圖形形狀的描述。由於物體的凸凹幾何形狀往往對其外形特徵有著決定性作用，而面實體的邊界線在某點的拱高正是對邊界線在該點的彎曲程度和凸凹性的反映。基於此，研究提出用一種基於拱高半徑複變函數的傅立葉形狀描述子來度量匹配實體之間的幾何形狀相似度，並選擇面實體的空間位置、形狀和大小等特徵，通過加權綜合構建面實體的綜合空間相似度度量模型，利用此模型進行矢量空間數據的匹配。
基於拱高半徑複變函數的傅立葉形狀描述
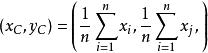拱高將幾何形狀邊界線用一個有序點集表示為S={p=(x，y)，i=1，2，…，n}，其中n為邊界線上的點數。取點集中所有點坐標的均值為邊界線的幾何中心點，記為C，則其坐標為
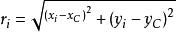拱高其中：x、y為邊界線上任一點的坐標。將邊界線上任一點pi到幾何中心點C的距離定義為邊界線在該點的半徑，記為ri，則有
將邊界線上任一點pi沿邊界線順時針方向和逆時針方向分別掃描弧長l(r/2)(l∈[0，L]，L為邊界線周長)，得到邊界線上兩點p和p，將點p到線段pp的距離定義為邊界線在該點的拱高，記為h，其中hi滿足下麵條件：線段pp在邊界線內時h>0，線段pp在邊界線外時h<0，如圖1所示。
基於綜合空間相似度度量模型的匹配步驟
根據所述相似度度量模型，研究採用雙向匹配方法，即先在B中查找與A中每一個實體匹配的目標，然後對B中沒有在A中找到匹配目標的每一個實體再在A中查找其匹配的目標。具體匹配步驟如下：
a)將不同來源、不同比例尺數據的坐標系進行統一。
b)通過待匹配實體的最小外接矩形確定該實體的候選匹配集。
c)獲取待匹配實體和候選匹配實體的中心位置和面積，並求取兩個實體的空間位置差異度和大小差異度。
d)提取待匹配實體和候選匹配實體邊界線，並根據設定弧長計算各個點半徑(即中心距離)和拱高，然後進行歸一化處理。
e)依據實體邊界線上各點的半徑和拱高組成的複數，對其進行快速傅立葉變換，取傅立葉變換係數的模組成向量，計算兩個實體特徵向量的歐氏距離，獲得兩個實體的形狀差異度。
f)多次提取已匹配實體對為正例樣本，計算各個差異度權值係數和綜合空間相似度閾值。
g)根據步驟c)和e)中所獲得的三個差異度和步驟f)中的權值係數，計算待匹配實體和候選匹配實體的綜合空間相似度，將候選匹配實體集中綜合空間相似度大於綜合空間相似度閾值者作為待匹配實體的匹配對象。
研究結論
面狀矢量要素匹配是矢量空間數據匹配和融合更新中最重要的一部分，要素實體的幾何特徵是決定匹配的關鍵。提出的基於拱高半徑複變函數的傅立葉形狀描述子，能夠有效地對要素實體幾何特徵進行描述，實驗結果表明，綜合匹配實體的位置、形狀和大小相似度的綜合空間相似度模型，能夠有效地實現同名實體的匹配，與其他算法相比，算法可以顯著提高匹配速度和減少漏匹配率，說明本文算法是正確有效的。
花崗岩殘積土邊坡水平拱高豎向變化規律
研究背景
我國山區面積約占全國陸地面積的三分之二，鐵路、公路向該類地區的延伸勢必造成大量的高路塹邊坡，樁與樁間措施的組合結構廣泛運用於高邊坡的加固中，如樁間牆、樁間板、樁間土釘牆等。樁間水平土拱效應是影響該類組合措施受力的關鍵因素。前人對樁間水平土拱進行了大量的研究，如通過室內模型實驗和數值模擬軟體，明確指出土拱效應的存在會影響砂性土應力釋放特性；通過理論計算分析，說明樁間水平土拱效應對樁間牆組合結構受力的影響；通過土壓力計量測土體自由應力場，證實了土拱效應會影響周圍土體的受力；由於考慮了土拱效應，得到的擋牆牆後主動土壓力的分布與模型試驗結果比較符合；通過現場大型試驗和室內模型實驗的監測研究工作，證實土拱效應影響了樁間板的土體受力；基於土拱效應，理論推導了疏排樁和土釘牆的相關計算公式，並通過實驗對公式進行了驗證；考慮摩擦拱的影響，隨著土體抗剪強度的增加相應樁間距可適當增加，隨著滑坡推力的增加相應樁間距應適當減小；通過數值模擬和模型實驗再現了土拱形成的過程；在土拱效應的前提下，提出了一種計算土壓力的新方法。大部分學者對土拱效應的研究大多集中在樁間距，如根據土拱的形狀、拱腳位置和假定的拱軸線方程，提出圓型抗滑樁的樁間距計算公式；從成拱原理出發，提出樁間距的簡便計算式；通過考慮樁土體的相關性質，建立了抗滑樁樁間距的計算公式。以上研究現狀表明，對土拱作用下的結構受力研究相對較少。現階段設計規範中庫侖主動土壓力的計算都沒有完全考慮土拱效應，因而沒有形成具體統一的計算方法，工程實踐中多依據設計單位，甚至設計人員個人的經驗進行，有以下幾種方法：
(1)不考慮土拱效應的影響，直接按照庫侖主動土壓力進行相關計算；
(2)間接考慮土拱效應，按庫侖主動土壓力進行相關計算時，依照以往工程經驗適當提高綜合內摩擦角(如5°左右)，使土壓力值得到一定程度的降低；
(3)折減庫侖主動土壓力值(如0.75倍左右)；
(4)考慮樁間板非完全剛性板，一定程度上具有柔性，設計樁間板時，板上荷載的土壓力參考卸荷拱內的土壓力值；
(5)樁間土釘牆的設計僅參考以往工程經驗取間距2～3m，約0.7倍牆高等長布置土釘。
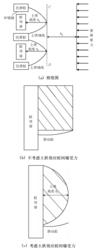圖2 樁間牆組合及樁間牆受力示意圖這些簡化計算方法有力地推動了土拱效應在工程設計中的套用，但均認為土拱效應在樁頂以下不同深度處土拱高度是不變的，完全沒有考慮水平土拱高度在樁頂以下不同深度的變化。其實，土拱高度在樁頂以下不同深度處的變化會影響上述組合措施的受力特徵，尤其是樁間結構上的受力。如圖2(a)所示(以樁間牆為例)，如不考慮土拱高度沿樁深方向的變化，作用於樁間措施(樁間擋土牆)的土壓力或剩餘下滑力由如圖2(b)所示範圍內的土體引起，考慮土拱的這種變化時，作用於樁間擋土牆上的土壓力或剩餘下滑力由如圖2(c)所示陰影部分土體引起。由於土體範圍不同，作用於該擋土牆的受力勢必會發生變化。
基於此，採用數值模擬方法對土拱高度沿樁深方向的變化進行系統研究，得出土拱高度沿樁深方向的變化規律，以期使考慮土拱效應的樁+樁間措施組合結構加固邊坡的工程設計更符合該類措施的實際受力。我國的花崗岩殘積土廣泛分布於東南沿海地區，華南、華東南地區分布尤其廣泛，其邊坡多採用抗滑樁進行加固，因此選擇花崗岩殘積土邊坡，並對其進行研究有著重要的現實意義。
土拱高度變化的數值模擬
（1）模型的建立
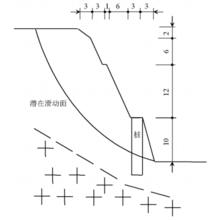圖3 邊坡剖面圖( 單位: m)FLAC3D是一種有限差分數值計算軟體，由於能構建滑坡模型以及提供適用於岩土體特性的本構模型，進而能夠較好地再現滑坡推力作用下的土拱效應，故採用FLAC3D軟體進行數值模擬，並採用Mohr-Coulomb準則。現階段大多數數值模型的建立是基於2根樁1個拱，實際工程中一般都是超過3根樁的，多根樁下生成的土拱是否對相鄰土拱高度造成影響，這方面的報導較少。本模型的建立採用4根樁，儘量消除多根樁情況下對相鄰土拱高度造成的影響，以擾動相對較小的中間拱高進行測量。選取G323邊坡作為數值模擬的研究對象，其當地地貌屬低丘陵，邊坡自然坡度為20°～50°，坡體介質為花崗岩風化殘積黏性土，殘留礫石一般為5%～7%，並含大量中、粗砂。砂、礫礦物成分為長石、石英，其餘組分為黏粒。該層土鑽孔揭露厚度50餘米，尚未揭穿。邊坡剖面如圖3所示。
（2）土拱效應數值模擬
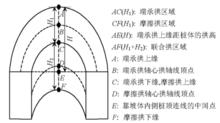圖4 土拱的分類在滑坡推力的作用下，土體會發生應力重分布，將滑坡推力分布到樁上或者樁側，發生土拱效應以穩定滑體，如圖4所示，土拱分為端承拱和摩擦拱，統稱為單獨拱，端承拱指滑坡推力集中在樁上形成的土拱，如圖4所示H1所在的區域，摩擦拱是樁側摩阻力平衡有效滑坡推力而形成的土拱，如圖4所示的H2區域，本文只研究端承拱，只考慮作用在樁上的滑坡推力形成的土拱範圍，以AE的高度H作為研究對象，進行相關的模擬和力學分析。
研究結論
(1)花崗岩殘積土沿樁深不同深度處土拱高度大小呈現減小的趨勢，通過FLAC3D數值模擬軟體和力學計算模型可知，樁頂以下不同深度處土拱高度越大，此處土拱跡線的應力等值線值越大，反之亦然，樁頂以下土拱高度變化原因是作用在樁上的力的差異及土體所受到的應力形成的應力等值線數值的差異。
(2)花崗岩殘積土邊坡水平土拱僅在樁頂以下4.5m深度範圍內，隨著深度的增加，力學計算的拱高變化幅度較數值模擬平緩。
(3)數值模擬通過中間拱與兩邊拱的傾斜度和拱形的差異，力學模型通過同一應力等值線下的中間拱與兩邊拱的高度差異說明樁頂以下3.0m範圍內相鄰樁對土拱造成了一定的影響，超過樁頂以下3.0m範圍，兩者的結果同時表明相鄰樁對土拱效應幾乎沒有影響，因此超過此範圍可不必考慮相鄰樁對土拱高度的影響。
(4)研究成果可套用於砂土類和碎石類等邊坡，即土拱未破壞前基本上處於彈性階段的土體所形成的邊坡，對於黏性土邊坡還有待進一步研究。
