敘述
拉克斯－米爾格拉姆定理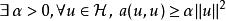
拉克斯－米爾格拉姆定理設是實希爾伯特空間，其內積記作，導出範數，是雙線性型，使得在上連續：，在上強制（有稱為 －橢圓性)： ，L是上的連續線性型。
那么存在唯一的，使得對所有都有：
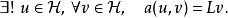拉克斯－米爾格拉姆定理而且如果a是對稱的，那么u是中唯一的元素，使得以下泛函取最小值，對所有，即：
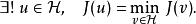拉克斯－米爾格拉姆定理證明
一般情形
套用里斯表示定理到連續線性型上，可知存在唯一的，使得對任意成立。
對所有，映射是上連續線性型，因此同樣可知存在唯一的，使得對任意成立。易知運算元是一個上連續線性自同態。由此可把表示成如下等價形式：
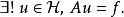拉克斯－米爾格拉姆定理要證明此命題，只要證得A是從到的 雙射。首先證明它是 單射，再證它是 滿射。
從a的強制性，使用柯西－施瓦茨不等式，得到對任何
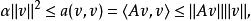拉克斯－米爾格拉姆定理從而知對任何
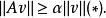拉克斯－米爾格拉姆定理這證明了A是單射。
要證明滿射，考慮運算元A在內的像。
不等式(*)表示，如是柯西序列，那么是內的柯西序列。由的完備性，收斂至。因A連續，得出收斂至。
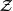拉克斯－米爾格拉姆定理因此為中的閉子空間，由投影定理可知。再設元素，從定義有，因此，故得。所以為，證得A是滿射。
自同態A是雙射，故在記憶體在唯一的u使得Au=f，且可以由得出。
附註
不用求出u，有其範數的上界估計
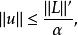拉克斯－米爾格拉姆定理其中表示對偶空間的範數。
對稱情形
如果雙線性型a對稱，那么對所有有：
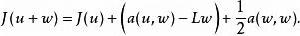拉克斯－米爾格拉姆定理因u是命題(1)的唯一解，有
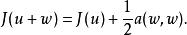拉克斯－米爾格拉姆定理從a的強制性有：
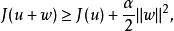拉克斯－米爾格拉姆定理
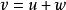拉克斯－米爾格拉姆定理
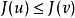拉克斯－米爾格拉姆定理
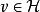拉克斯－米爾格拉姆定理取 ，從上式有 對任意 成立。
套用
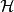拉克斯－米爾格拉姆定理 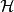拉克斯－米爾格拉姆定理
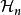拉克斯－米爾格拉姆定理
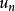拉克斯－米爾格拉姆定理這定理是有限元法的基礎。實際上，若不在 內求u，而是在 的有限n維子空間 內求 ，那么
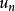拉克斯－米爾格拉姆定理如果a對稱，以a為內積， 是u的投影。
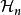拉克斯－米爾格拉姆定理
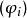拉克斯－米爾格拉姆定理給出 的基 ，上述問題化為求解線性方程組：
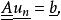拉克斯－米爾格拉姆定理
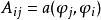拉克斯－米爾格拉姆定理
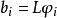拉克斯－米爾格拉姆定理其中 ， 。
