拉伸檢測試驗方法
 圖1
圖1 圖2
圖2試驗中所採用的試樣要么具有圓形橫截面,要么具有矩形橫截面,試樣兩端尺寸通常要加大,以保證夾持部位具有更大的面積,從而避免試樣在夾持部位發生斷裂。圖1和圖2所示為幾種金屬材料和高分子材料試驗前和試驗後的試樣照片。
試樣兩端的夾持方法隨著試樣的幾何形狀而變化。圖3所示為帶有螺紋試樣的典型布置圖。可以注意到,每端都使用球形軸承來提供一個純粹的拉伸載荷,沒有不合需要的彎曲。進行試驗的一般方式就是以一個恆定速度使試樣發生變形。例如,在圖4所示的萬能試驗機上,固定十字頭和驅動十字頭之間的運動可以控制成一種恆定速度。因此,圖4中的距離h是變化的,因而dh/dt=h為常數。
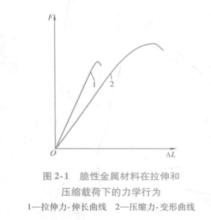 圖4
圖4在進行試驗的過程中,為獲得這一位移速率而必須施加的軸向載荷是變化的。載荷P除以橫截面面積A就可以獲得試樣在試驗過程中任意時刻的應力,則有:
σ=P/A
試樣的位移是在標距長度L上具有恆定橫截面面積的中間直線部分測得的,如圖3所示。應變ε可以由這個標距長度變化△L計算出來,則有:
ε=△L/L
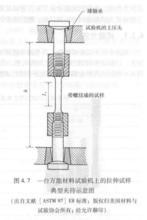 圖3
圖3就像前面所描述的一樣,以原始尺寸(未變形時的尺寸)A和L為基礎計算的應力和應變稱為工程應力和工程應變。
有時假設所有夾持部分和試樣末端幾乎都是剛性的,這是合理的。在該種情況下,十字頭運動中發生的大部分變化是由於試樣直線部分的變形而引起的,因而△L與h的變化△h幾乎相同,因而可以將應變估算為ε=△h/L。然而,實際測量的△L值是優先選用的,因為使用△h可能會導致所測應變值產生很大的誤差。
從式(2)中所計算的應變ε是無量綱的。為了方便起見,應變有時會以百分數的形式給出,此時ε=100。應變也可以用百萬分之一表示,稱為微應變,此時ε=10 ε。如果應變是以百分數或者微應變的形式給出的,則對於大多數計算來說,在使用該值之前,有必要將其轉換成無量綱的ε形式。
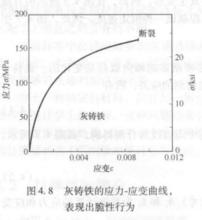 圖5
圖5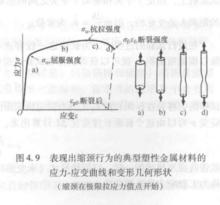 圖6
圖6由拉伸試驗所獲得的主要結果就是整個試驗的工程應力,工程應變曲線圖,稱為應力一應變曲線。由於在實驗室中使用數字計算機,數據的形式就是一個應力和應變數值列表,是在試驗期間以很短的時間間隔取樣而獲得的。應力一應變曲線因材料不同而變化很大。在拉伸試驗中的脆性行為就是材料沒有發生大的變形就失效了。灰鑄鐵、玻璃和一些高分子材料(如PMMA)就是脆性材料的例子。圖5所示為灰鑄鐵的應力一應變曲線。其他的材料則表現出了塑性行為,在拉伸載入中只有在發生很大的變形之後才失效。工程金屬材料和一些高分子材料的塑性行為的應力一應變曲線如圖6和圖7所示 。
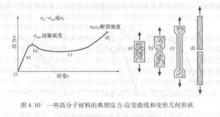 圖7
圖7補充說明
值得注意的是,對於一種給定材料的具有不同橫截面A的試樣,隨著橫截面面積的增加,其失效載荷也會隨之而增加。通過計算每單位面積的載荷(或稱為應力),就會消除試樣尺寸的影響。因此,對於一種給定的材料,對於任意橫截面面積A,都有望具有相同的屈服應力、極限應力和斷裂應力,然而相應的載荷P則隨著橫截面面積A而變化。事實上,對不同A下的試驗進行比較時,其結果會受到原始材料不同位置性能的微小差異的影響,在實驗室測量時缺乏絕對的精度,而且還存在統計誤差。使用應變ε同樣會消除試樣長度的影響。對於一給定應力,長度L更大的試樣,就會按比例表現出更大的長度變化△L,但是對於任何長度的試樣而言,與屈服應力、極限應力和斷裂應力點相對應的應變都期望是相同的。因此,應力—應變曲線被認為能夠基本描述材料的力學行為 。

