基本介紹
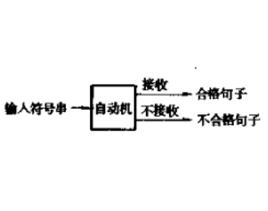
抽象自動機是一種能夠識別語言的抽象的裝置,它不是具有物理實體的機器,而是表示計算機運算方式的抽象的邏輯關係系統,這樣的抽象自動機可以用來檢驗輸入的符號串是不是語言中合格的句子,如果是合格的句子,自動機就接收它,如果不是,就不接收它,如圖所示:
 圖1 抽象自動機
圖1 抽象自動機數理語言學中研究抽象自動機的理論稱為自動機理論(automata theory)。
抽象自動機的分類
自動機可分為有限自動機(即時序機)、後進先出自動機(即下推自動機)、線性有界自動機、圖靈機等幾種。它們對語言的識別能力各不相同。
自動機理論是以研究離散數學系統的結構、功能以及兩者之間關係為主要內容的數學理論。自動機有11種: 有限自動機、下推自動機、線性有界自動機、圖靈機、時序機、波斯特機、隨機存取機、堆疊自動機、無線自動機、機率自動機和細胞自動機。
常見自動機有以下幾種:以電話交換機為主要實例的有限自動機,是自動機理論的基礎,被套用到自動控制、生物系統中;由下推表組成的單項非確定程式的下推自動機;線性有界自動機;用來描述通用計算機計算能力的圖靈機模型;進行與轉移函式,轉移狀態有關輸出的時序機;由一些基本語句構成程式框圖的波斯特機;隨機存儲機;堆疊自動機;不受有限自動機做控制器和存儲限制的無限自動機;統計自動機某一條件機率分布的機率自動機和細胞自動機。
有限自動機
有限自動機(finite automaton)亦稱時序機,有限離散數字系統的抽象數學模型。一個有限自動機M由五元組(X,Y,S,δ,λ)給定,其中X,Y和S都是非空有限集,分別稱為M的輸入集、輸出集和狀態集;δ是笛卡兒積集合S×X到S的映射,稱為M的下一狀態函式;λ是S×X到Y的單值映射,稱為M的輸出函式,當δ是單值映射時,稱M為 確定型有限自動機;當δ是多值映射時,稱M為 非確定型有限自動機。有限自動機有三種功能:作為序列轉換器,將輸入序列變換為輸出序列;作為序列識別器,識別輸入的序列是否具有某種性質;作為序列產生器,產生具有所要求性質的序列 。
研究有限自動機的功能、結構以及兩者關係的數學理論稱為有限自動機理論。有限自動機理論的基本內容包括邏輯網路、狀態化簡、狀態分配、神經網路和有限識別器等。
1.邏輯網路。基本的邏輯元件按是否具有記憶功能,可以分為記憶元件(如觸發器和延遲器等)和組合元件(如各種與、或、非門等)兩類。把一些基本邏輯元件按一定要求連結起來,就組成邏輯網路。若把邏輯網路中進入記憶元件的輸入線去掉後所得網路不再含有迴路,則稱這樣的網路為合式網路。不含記憶元件的合式網路稱組合網路。邏輯網路比組合網路複雜。在工程實現上,要求對於一個給定的有限自動機建立和實現此有限自動機的邏輯網路。已經證明任何合式網路的功能都可以用一個有限自動機來描述;任何一個有限自動機描述的功能也都可以用合式網路來實現。
2.狀態化簡。對任何有限自動機都惟一(在同構意義下)存在一個狀態數目最少的有限自動機與它等價。根據有限自動機理論,對給定的有限自動機,可有效地求出與之等價的最簡形式的有限自動機。
3.狀態分配。要構造具有多個狀態的網路,需要使用多個基本記憶元件,利用這些記憶元件的各種狀態組合來表示不同的狀態。一般地,不同的狀態分配導致邏輯網路具有不同的複雜程度.如何選擇較好的分配方案,使邏輯網路的構造儘可能地簡單,是有限自動機研究的一個主要課題。
4.神經網路。1943年,麥克卡洛克(Mcculloch)和皮特斯(W.Pitts)提出的神經網路模型是有限自動機的一個實例。1951年,克林(S.C.Kleene)在這種神經網路模型的基礎上,提出了正則事件(正則語法)的概念,證明了正則事件是可以被神經網路或有限自動機表示的事件,而且神經網路或有限自動機可以表示的事件也一定是正則事件。
5.有限識別器。在形式語言理論中,有限自動機通常作為語言的識別器來使用。作為識別器,有限自動機的輸出可以被忽略,而由最後達到的狀態去決定輸入序列是否具有給定的性質,這種有限自動機也稱為有限接收機。按其下步狀態是否完全確定,有限識別器可分為確定型和非確定型兩種,它們分別與確定型和非確定型有限自動機相對應,它們也都接受同一類語言,即正則語言 。
機率自動機
機率自動機(probabilistic automaton)亦稱 隨機自動機,一種自動機。是所處環境或內部具有有限或無限的隨機因素的自動機,與非機率型自動機的主要區別是:機率自動機的動作是隨機的.每個機率自動機一般都需規定兩組機率:一是給定自動機的初始狀態的機率分布——初始分布,一般用一個隨機矢量表示;二是規定在自動機處於某一狀態,並向自動機輸入某個字母的條件下,自動機下一動作(如狀態轉移、輸出某個字母、改寫字母等)的條件機率函式。有了這兩組機率,就可計算自動機到達某個最終狀態的機率,包含有不可靠元件的數字電路和通信的信道都可以表示為機率自動機。
細胞自動機
細胞自動機(cellular automaton)是一種自動機,是有限細胞空間形式的自動機,常作為並行計算機的一種理論模型,細胞空間概念是馮·諾伊曼(J.von Neumann)在20世紀50年代初期研究自繁殖自動機的邏輯問題時提出的,細胞自動機由許多細胞(或單元)構成。每個“細胞”是一台計算機的模型,都有自己的存儲器,都具有輸入、加工和輸出數據的能力。細胞和細胞之間有鄰接關係,有些模型還和外部相連,以便與外部交換輸入輸出數據。馮·諾伊曼細胞自動機是最早最基本的自動機,其他各種類型的細胞自動機(如L系統)都是由馮·諾伊曼自動機推廣而來的。細胞自動機除了在形式上可作為並行計算機的理論模型來研究外,還可以作為語言(被機器接受的輸入字的集合)識別器,用於模式識別.此外,它對於大規模積體電路的設計方法也具有重要的意義。
下推自動機
下推自動機(pushdown automaton)亦稱 後進先出自動機,一種自動機。是能控制一條輸入帶和一個棧的有限自動機。棧也稱為“後進先出”表,即符號的寫入或取出只能在表的頂端進行。在文法結構數學模型中,下推自動機可以用作上下文無關語言的識別接受器。下推自動機(簡稱PDA)可以形式地定義為一個7元組P=(Q,Σ,Γ,δ,q,Z,F),其中:
1.Q是一個有限的狀態集合;
2.Σ是一個有限的輸入字母表;
3.Γ是一個有限的棧字母表;
4.δ是一個從Q×(Σ∪{e})×Γ到Q×Γ*的有限子集的映射;
5.q在Q中,是有限控制的初始狀態;
6.Z在Γ中,是一個稱為棧底的符號;
7.F⊆Q,是終結狀態集合。
下推自動機是一個非確定的裝置,對於有限自動機,確定型和非確定型有限自動機在接受語言上是等價的。這一結論對於下推自動機是不成立的。非確定型下推自動機接受的語言集合是上下文無關語言;確定型下推自動機接受的語言集合是非確定型下推自動機接受的語言集合的真子集,稱為確定型上下文無關語言。
圖靈機
圖靈機(Turing machine)是一種抽象計算模型,是20世紀30年代中期英國數學家圖靈(A.M.Turing)首先提出來的,用來精確定義可計算函式,圖靈機由一個控制器、一條可無限延伸的存儲帶和一個讀寫頭組成,它所能進行的操作為:
1.左移(讀寫頭在存儲帶上向左移一格);
2.右移;
3.在存儲帶的某一格內寫下或清除一個符號;
4.條件轉移等。
圖靈機的結構雖然比較簡單,但在理論上它卻能夠模擬現代數字計算機的一切運算,因此可看作是現代數字計算機的一種數學模型。可以通過對這種模型的研究來揭示數字計算機的性質.可以證明,存在一個圖靈機U,它可以模擬任何其他圖靈機,這樣的圖靈機U稱為通用圖靈機。通用圖靈機正是後來出現的存儲指令的通用數字計算機的理論原型.圖靈機所定義的語言類稱為遞歸可枚舉集.圖靈機所計算的整數函式類稱為部分遞歸函式。圖靈機在計算能力上等價於遞歸函式、波斯特系統等其他計算模型。
線性有界自動機
線性有界自動機(linear bounded automaton)是一種圖靈機(參見“圖靈機”),是把計算限制在僅僅包含輸入的那一段帶上的圖靈機,可用作上下文有關語言的識別接受器。線性有界自動機(縮寫為LBA)可形式地由M=(K,Σ,Γ,δ,q,F)來表示,其中:K是狀態的有限集;Γ是帶符號的有限集;Σ⊆Γ是輸入符號集;K中的q是起始狀態;F⊆K是終結狀態集;δ是從K×Γ到K×Γ×{L,R}子集的映射,(L,R)分別是讀寫頭左右移一格。Σ含有兩個特殊的符號,通常記為¢和$,它們分別是左端標誌和右端標誌。這些符號開始就處在輸入帶的端點,其作用是阻止帶頭離開帶上出現符號的區。
確定型和非確定型圖靈機接受的語言是相同的,但是,已知非確定型線性有界自動機(以NDLBA表示)接受的語言類正好是上下文有關語言。確定型線性有界自動機(以DLBA表示)的功能不會超過NDLBA的,以不等式表示為
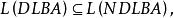 抽象自動機
抽象自動機其中L表示該類自動機接受的語言集合,至今人們仍未能把包含關係精確為真包含關係或相等關係,這是一個著名的尚未解決的問題,簡稱LBA問題 。
自動機理論
自動機理論(automaton theory)是關於自動機的功能、結構及兩者關係的數學理論。自動機是一個數學概念,它是離散數字系統的抽象模型,這裡所說的離散數字系統,乃是一種動態系統,它的變數是數字量,時間是離散的。例如,數字電路和算法就是兩個典型的離散數字系統。自動機理論的主要研究課題是分析和綜合問題:給出一個具體的自動機的結構,分析它的功能;給出自動機的功能描述,綜合出能實現此功能的自動機的結構。
自動機理論是理論計算機科學中較早形成的部分,早在1850年,英國布爾(G.Boole)就在用數學方法研究思維規律的問題時,建立了邏輯代數。1948年,美籍匈牙利數學家馮·諾伊曼(J.von Neumann)提出建立自動機的一般邏輯理論。20世紀50年代,在開關網路理論和數理邏輯中圖靈機理論的基礎上,形成了自動機理論這一數學分支學科。20世紀50年代以來,自動機理論有了深入的發展和廣泛的套用。自動機理論大致可分為以下五個次級學科:
1.有限自動機理論:主要研究對象為開關網路、數字電路、計算機這類存儲量有限的自動機;
2.無限自動機理論:主要研究對象為算法和理想計算機這類存儲量不受限制的自動機;
3.機率自動機理論:主要研究對象是在環境或內部具有隨機因素的自動機;
4.細胞自動機理論:主要研究對象是由許多互連的小自動機並行運算形成的大自動機;
5.抽象自動機理論:將自動機作為一種數學系統,研究自動機的一般數學性質。
自動機理論與數理邏輯、可計算性理論、計算複雜性理論、形式語言理論、控制論等數學分支都有關係,特別是它與形式語言理論關係密切。一方面自動機作為形式語言的一種主要描述方法,另一方面形式文法也可作為自動機識別集的一種描述方法。自動機理論在自動控制、計算機和數字通信等領域有著廣泛的套用 。
美國語言學家N.喬姆斯基等人建立了形式文法和自動機之間的聯繫,證明語言的形式文法與自動機之間存在著如下的對應關係:①若某一語言能用圖靈機來識別,則它就能用O型文法生成,反之亦然;②若某一語言能用線性有界自動機來識別,則它就能用上下文敏感文法生成,反之亦然;③若某一語言能用後進先出自動機來識別,則它就能用上下文自由文法生成,反之亦然;④若某一語言能用有限自動機來識別,則它就能用有限狀態文法生成,反之亦然。
這種關於形式文法與自動機的關係。反映了語言的生成過程與識別過程的內在聯繫,它已成為計算機科學的基石之一,這是語言學對於現代自然科學發生影響的一個明證 。