簡介
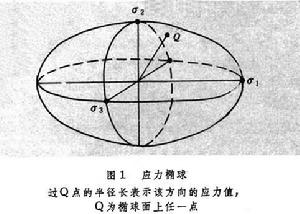
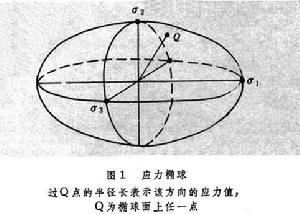
以3個主應力軸作橢球體的3個軸來描述受力物體內一點中各截面上的應力的橢球體。應力橢球面上某一點至橢球心的矢量表示某一方向截面上的應力矢量。如圖1所示。除了與主應力平行的矢量外,其他應力矢量都不是作用在與其相垂直的平面上，也就是說它們都不是正應力，而具有剪下分量。
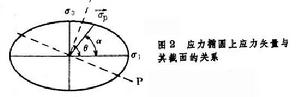
應力橢球體以平面的應力橢圓為例(圖2)，
應力橢球體σ1和σ3分別為最大和最小主應力，設一平面P，其法線方向與σ1成θ角，則作用於平面P上的應力矢量
與σ1的夾角為α,
, 沿方向上的橢圓半徑為的值。在以σ1及σ3為X及Y軸坐標上的分量σX及σY滿足下列方程式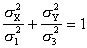
在以 3個主應力軸(σ1,σ2,σ3)為X，Y，Z軸的正交坐標系中，應力橢球的方程式為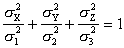
其中σX，σY,σZ為作用於截面P上的應力矢量在 3個軸上的分量。
地質體中3軸受壓的應力條件比較普遍,所以應力符號常規定壓為正，拉為負。應力橢球的軸長通常表為正的應力值，但遇到某一軸為拉應力時，不能以負的軸長表示橢球的實體，從而限制了應力橢球的套用範圍。
