感知器[神經網路模型]

感知器是人工神經網路中的一種典型結構， 它的主要的特點是結構簡單，對所能解決的問題 存在著收斂算法，並能從數學上嚴格證明，從而對神經網路研究起了重要的推動作用。

感知器，也可翻譯為 感知機，是 Frank Rosenblatt在1957年就職於Cornell航空實驗室(Cornell Aeronautical Laboratory)時所發明的一種人工神經網路。它可以被視為一種最簡單形式的前饋式人工神經網路，是一種二元線性分類器。

Frank Rosenblatt給出了相應的感知器學習算法，常用的有感知機學習、最小二乘法和梯度下降法。譬如，感知機利用梯度下降法對損失函式進行極小化，求出可將訓練數據進行線性劃分的分離超平面，從而求得感知器模型。

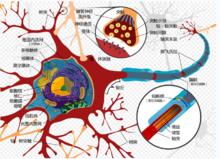圖1.神經細胞示意圖

感知器是生物神經細胞的簡單抽象，如右圖.神經細胞結構大致可分為：樹突、突觸、細胞體及軸突。單個神經細胞可被視為一種只有兩種狀態的機器——激動時為‘是’，而未激動時為‘否’。

神經細胞的狀態取決於從其它的神經細胞收到的輸入信號量，及突觸的強度（抑制或加強）。當信號量總和超過了某個閾值時，細胞體就會激動，產生電脈衝。電脈衝沿著軸突並通過突觸傳遞到其它神經元。為了模擬神經細胞行為，與之對應的感知機基礎概念被提出，如權量（突觸）、偏置（閾值）及激活函式（細胞體）。

在人工神經網路領域中，感知器也被指為單層的人工神經網路，以區別於較複雜的多層感知器（Multilayer Perceptron）。 作為一種線性分類器，（單層）感知器可說是最簡單的前向人工神經網路形式。儘管結構簡單，感知器能夠學習並解決相當複雜的問題。感知器主要的本質缺陷是它不能處理線性不可分問題。

起源

1943年，心理學家Warren McCulloch和數理邏輯學家Walter Pitts在合作的《A logical calculus of the ideas immanent in nervous activity》論文中提出並給出了人工神經網路的概念及人工神經元的數學模型，從而開創了人工神經網路研究的時代。 1949年，心理學家唐納德·赫布在《The Organization of Behavior》論文中描述了神經元學習法則。

感知器

人工神經網路更進一步被美國神經學家 Frank Rosenblatt 所發展。他提出了可以模擬人類感知能力的機器，並稱之為‘感知機’。1957年，在 Cornell 航空實驗室中，他成功在IBM 704機上完成了感知機的仿真。兩年後，他又成功實現了能夠識別一些英文字母、基於感知機的神經計算機——Mark1，並於1960年6月23日，展示與眾。

為了‘教導’感知機識別圖像，Rosenblatt，在Hebb 學習法則的基礎上，發展了一種疊代、試錯、類似於人類學習過程的學習算法——感知機學習。除了能夠識別出現較多次的字母，感知機也能對不同書寫方式的字母圖像進行概括和歸納。但是，由於本身的局限，感知機除了那些包含在訓練集裡的圖像以外，不能對受干擾（半遮蔽、不同大小、平移、旋轉）的字母圖像進行可靠的識別。

首個有關感知器的成果，由 Rosenblatt 於1958年發表在《The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain》的文章里。1962年，他又出版了《Principles of Neurodynamics: Perceptrons and the theory of brain mechanisms》一書，向大眾深入解釋感知機的理論知識及背景假設。此書介紹了一些重要的概念及定理證明，例如感知機收斂定理。

感知器

雖然最初被認為有著良好的發展潛能，但感知機最終被證明不能處理諸多的模式識別問題。1969年，Marvin Minsky 和 Seymour Papert 在《Perceptrons》書中，仔細分析了以感知機為代表的單層神經網路系統的功能及局限，證明感知機不能解決簡單的異或（XOR）等線性不可分問題，但 Rosenblatt 和 Minsky 及 Papert 等人在當時已經了解到多層神經網路能夠解決線性不可分的問題。

由於 Rosenblatt 等人沒能夠及時推廣感知機學習算法到多層神經網路上，又由於《Perceptrons》在研究領域中的巨大影響，及人們對書中論點的誤解，造成了人工神經領域發展的長年停滯及低潮，直到人們認識到多層感知機沒有單層感知機固有的缺陷及反向傳播算法在80年代的提出，才有所恢復。1987年，書中的錯誤得到了校正，並更名再版為《Perceptrons - Expanded Edition》。

在 Freund 及 Schapire (1998)使用核技巧改進感知器學習算法之後，愈來愈多的人對感知機學習算法產生興趣。後來的研究表明除了二元分類，感知機也能套用在較複雜、被稱為 structured learning 類型的任務上（Collins, 2002），又或使用在分散式計算環境中的大規模機器學習問題上（McDonald, Hall andMann,2011）。

數學描述

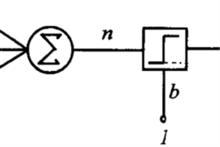
感知器使用特徵向量來表示的前饋式人工神經網路，它是一種二元分類器，把矩陣上的輸入（實數值向量）映射到輸出值 上（一個二元的值）。

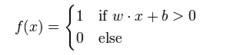數學表達式

感知器[神經網路模型]

感知器[神經網路模型]

感知器[神經網路模型]

是實數的表式權重的向量， 是點積。 是偏置，一個不依賴於任何輸入值的常數。偏置可以認為是激勵函式的偏移量，或者給神經元一個基礎活躍等級。

感知器[神經網路模型]

感知器[神經網路模型]

(0 或 1)用於對進行分類，看它是肯定的還是否定的，這屬於二元分類問題。如果 是負的，那么加權後的輸入必須產生一個肯定的值並且大於 ，這樣才能令分類神經元大於閾值0。從空間上看，偏置改變了決策邊界的位置（雖然不是定向的）。

由於輸入直接經過權重關係轉換為輸出，所以感知機可以被視為最簡單形式的前饋式人工神經網路。

算法改進

附加動量法

它在標準的 BP 算法修正 權值時，在每一個權重的變化上加上一項動量因 子，動量因子正比於上一次權重變化量的值，並 根據反向傳播法來產生新的權重的變化。在沒有 附加動量的作用下，網路可能陷入局部極小值， 利用附加動量的作用有可能跳過這些極小值。這 是因為附加動量法在修正其權值時，考慮了在誤 差曲面上變化趨勢的影響，從而抑制了局部極小， 找到誤差曲面的全局最小值。這裡動量因子實質 上起到了緩衝的作用，它減小了學習過程的振盪 現象，一定程度上加快了 BP 算法的收斂速度。

速率算法

標準 BP 算法的 學習速率採用的是確定值，學習速率的選擇非常 重要，學習速率選得小雖然有利於總誤差縮小， 但會導致收斂速度過慢。學習速率選取得太大， 則有可能導致無法收斂。為了解決這一問題，可 以採用自適應調整學習效率的改進算法，此算法 的基本思想是根據誤差變化而自適應調整。如果 權值修正後確實降低了誤差函式，則說明所選取 的學習速率值小了，應增大學習速率; 如果沒有則說明學習速率調得過大，應減 國小習速率。總之使權值的調整向誤差減小的方 向變化。自適應學習速率算法可以縮短訓練時間。

速率調整算法

這一 算法採用了附加動量法和自適應學習速率法兩種 方法的結合，既可以找到全局最優解，也可以縮 短訓練時間。此外，還有學者提出了隱含層節點 和學習效率動態全參數自適應調整等算法，有效 地改善了收斂效果。 另一類 BP 改進算法是對其進行了數學上的優 化，如擬牛頓法在搜尋方向上進行了改進; 共軛梯度法則是在收斂速度和計算複雜度上均能取得 較好效果，特別是用於網路權值較多的情形 ; Levenberg － Marquardt 法則結合了梯度下降和牛 頓法的優點，在網路權值不多的情形下，收斂速 度很快，優點突出。