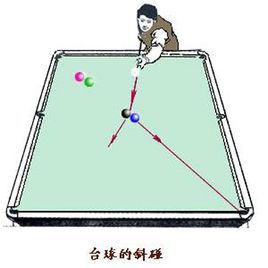
彈性斜碰
彈性斜碰本公式套用條件:①完全彈性碰撞,無能量損失。②都是剛性等直徑的小球。③衝擊球有速度,而受擊球靜止。
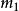 彈性斜碰
彈性斜碰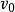 彈性斜碰
彈性斜碰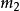 彈性斜碰
彈性斜碰 彈性斜碰
彈性斜碰題設:設質量為 的小球具有速度 ,質量為 的小球靜止,沿初速度方向運動到處,兩球相切,設兩球心所在直線方向和衝擊球初速度方向夾角銳角為α,求兩球的末速度大小 ,以及初速度方向和衝擊球末速度方向夾角θ。
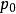 彈性斜碰
彈性斜碰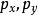 彈性斜碰
彈性斜碰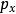 彈性斜碰
彈性斜碰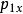 彈性斜碰
彈性斜碰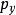 彈性斜碰
彈性斜碰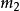 彈性斜碰
彈性斜碰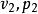 彈性斜碰
彈性斜碰解:如右圖,將初動量 沿球心和其正交方向分解為 ,碰後的分動量 變成 ,而 不變, 獲得 ,有動量守恆和能量守恆有關係式:
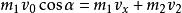 彈性斜碰
彈性斜碰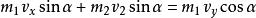 彈性斜碰
彈性斜碰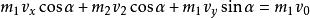 彈性斜碰
彈性斜碰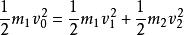 彈性斜碰
彈性斜碰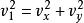 彈性斜碰
彈性斜碰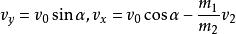 彈性斜碰
彈性斜碰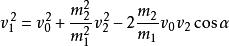 彈性斜碰
彈性斜碰設從上到下分別設成式子①②③④⑤,由①②聯立得到 ,又有式子5得到 ,將其代入式子4中,可以得到:
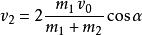 彈性斜碰
彈性斜碰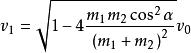 彈性斜碰
彈性斜碰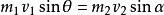 彈性斜碰
彈性斜碰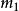 彈性斜碰
彈性斜碰又由於總動量在縱方向為0,所以可知 。代入兩個速度值,可求 的末速度方向
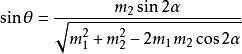 彈性斜碰
彈性斜碰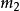 彈性斜碰
彈性斜碰 彈性斜碰
彈性斜碰而得 末速度方向仍沿 方向運動。
特別的;當兩球質量相等時,兩球的末速度方向必然相互垂直。而且有速度公式:
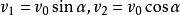 彈性斜碰
彈性斜碰套用
在實際生活中,兩球質量相等的二維彈性碰撞,檯球就是很好的例子,完全符合此公式。在核物理學中,粒子和原子核等發生碰撞,都是這樣的模型。